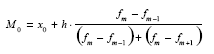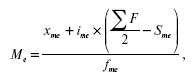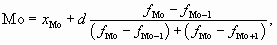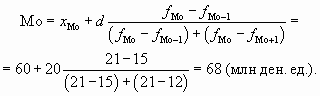структурные средние мода и медиана
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:
где х о – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1 – частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:

где хо – нижняя граница медианного интервала;
NМе – порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число | ||||
| До 5000 | 600 | 600 | 6 | ||
| 5000-6000 | 700 | 1300 (600+700) | 13 | ||
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 ) (хо) | 2500 (fМе) | 5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 | ||
| 9000-10000 | 1500 | 9200 | 92 | ||
| Свыше 10000 | 800 | 10000 | 100 | ||
| Итого | 10000 | – | – |
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если М о о следует сделать вывод о левосторонней асимметрии ряда.
3. Структурные средние величины. Мода и медиана
3. Структурные средние величины. Мода и медиана
Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.
Мода (М о ) – чаще всего встречающийся вариант. Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений.
Мода представляет наиболее часто встречающееся или типичное значение.
Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен.
В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность).
В пределах интервала надо найти то значение признака, которое является модой.
где х о – нижняя граница модального интервала;
h – величина модального интервала;
f m – частота модального интервала;
f т —1 – частота интервала, предшествующего модальному;
f m +1 – частота интервала, следующего за модальным.
Мода зависит от величины групп, от точного положения границ групп.
Мода – число, которое в действительности встречается чаще всего (является величиной определенной), в практике имеет самое широкое применение (наиболее часто встречающийся тип покупателя).
Медиана (M e – это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.
Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения.
Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.
Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал:
где х ме– нижняя граница медианного интервала;
i Me – величина медианного интервала;
f/2 – полусумма частот ряда;
S Me —1 – сумма накопленных частот, предшествующих медианному интервалу;
f Me – частота медианного интервала.
Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Структурные продукты
Структурные продукты Блог об инвестициях с ограниченным риском –
МОДА НА ИНВЕСТИЦИИ
Структурные проблемы?
Структурные проблемы? Я убежден, что наша нынешняя система обеспечения рабочей силой необыкновенно негибка и не подготовлена к решению каких бы то ни было задач. Она не способна адекватно реагировать на возможности, которые может предложить промышленность. Это создает
Структурные подразделения
Структурные подразделения В небольшой организации каждый сотрудник может выполнять ту или иную функцию или совмещать несколько функций. По мере увеличения численности уже несколько работников начинают выполнять те же самые или подобные обязанности. На этом этапе
23. Средние величины и общие принципы их исчисления
23. Средние величины и общие принципы их исчисления Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количе–ства индивидуальных
25. Мода и медиана
25. Мода и медиана Мода – величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда. Она показывает размер признака, свойственный значи–тельной
ЛЕКЦИЯ №5. Средние величины и показатели вариации
ЛЕКЦИЯ №5. Средние величины и показатели вариации 1. Средние величины и общие принципы их исчисления Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на
1. Средние величины и общие принципы их исчисления
1. Средние величины и общие принципы их исчисления Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений
59. Относительные и средние величины
59. Относительные и средние величины Экономический анализ начинается по своей сути с исчисления величины относительной. Относительные величины незаменимы при анализе явлений динамики. Понятно, что эти явления можно выразить и в абсолютных величинах, но доходчивость,
4.3.1 Структурные реформы
4.3.1 Структурные реформы В перспективе для серьезного улучшения инвестиционного климата в России, роста производства и производительности исключительно важно выравнивание условий конкуренции и дальнейшая либерализация экономики. Неэффективные предприятия не должны
ЛЕКЦИЯ № 7. Средние величины
ЛЕКЦИЯ № 7. Средние величины 1. Общая характеристика В целях анализа и получения статистических выводов по результатом сводки и группировки исчисляют обобщающие показатели – средние и относительные величины.Задача средних величин – охарактеризовать все единицы
3. Структурные средние величины. Мода и медиана
3. Структурные средние величины. Мода и медиана Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.Мода (Мо ) – чаще всего встречающийся вариант. Модой называется
Мотоциклы, высокая мода и карнавал
Мотоциклы, высокая мода и карнавал Шоу Кренза 1997 года превратило освященный белыми рамами Гуггенхейм в место стоянки сотен блестящих, новеньких мотоциклов, которые представляли собой «новаторские стили» столетия[91]. Классические художественные школы были возмущены; они
18.4.5.2. Медиана репутации
18.4.5.2. Медиана репутации Как обсуждалось в предыдущем разделе, репутация, измеренная через среднее арифметическое (или соответствующие суммы) оценок, может быть хорошим показателем репутации. Тем не менее он все еще далек от преодоления уклона репутации, производимого
Основная мода России
Основная мода России Если вам кажется, что ситуация улучшается, значит, вы чего-то не заметили.Со страной нужно находиться в резонансе, так чтобы «быть в струе», чтобы окружающее пространство не сопротивлялась вам, а помогало, чтобы продвижение вперед происходило бы
Теория статистики.
31. Структурные средние величины. Мода и медиана.
Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.
Мода (Мо) – чаще всего встречающийся вариант.
Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений.
Мода представляет наиболее часто встречающееся или типичное значение. Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен.
В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность). В пределах интервала надо найти то значение признака, которое является модой.
Где х0– нижняя граница модального интервала;
h– величина модального интервала;
fm– частота модального интервала;
fm+ 1 – частота интервала, следующего за модальным.
Мода зависит от величины групп, от точного положения границ групп.
31б Мода – число, которое в действительности встречается чаще всего (является величиной определенной), в практике имеет самое широкое применение (наиболее часто встречающийся тип покупателя).
Медиана (Ме)– это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.
Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения.
Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.
Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал:
Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.
Структурные средние величины. Мода и медиана
Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.
Мода (Мо) – чаще всего встречающийся вариант.
Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений.
Мода представляет наиболее часто встречающееся или типичное значение. Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен.
В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность). В пределах интервала надо найти то значение признака, которое является модой.
где x0– нижняя граница модального интервала;
h– величина модального интервала;
fm– частота модального интервала;
fm+ 1 – частота интервала, следующего за модальным.
Мода зависит от величины групп, от точного положения границ групп.
Мода – число, которое в действительности встречается чаще всего (является величиной определенной), в практике имеет самое широкое применение (наиболее часто встречающийся тип покупателя).
Медиана (Me)– это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.
Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения.
Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.
Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал:
Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.
Структурные характеристики вариационного ряда распределения
8.1. Мода
8.1.1. Определение моды в дискретных вариационных рядах
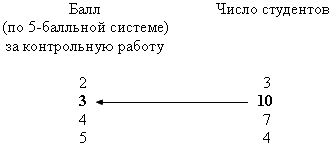
В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, которому соответствует наибольшая частота, и будет значением моды.
Пример 8.1. По представленным ниже результатам проведения контрольной работы по статистике определим моду.
8.1.2. Определение моды в интервальных вариационных рядах с равными интервалами
Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле
Пример 8.2. Имеются данные по группе банков.
| Сумма выданных кредитов, млн ден. ед. | Количество банков |
|---|---|
| До 40 | 8 |
| 40-60 | 15 |
| 60-80 | 21 |
| 80-100 | 12 |
| 100-120 | 9 |
| 120-140 | 7 |
| 140 и выше | 4 |
| Итого | 77 |
Определим модальный размер выданных кредитов:
Подставив в формулу соответствующие величины, получим
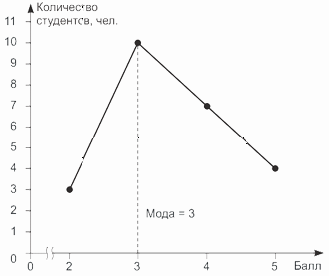
Пример 8.3. По результатам проведения контрольной работы по статистике, приведенным в примере 8.1, определим моду графическим способом.
Для этого построим полигон распределения и найдем абсциссу его вершины (рис. 8.1).
Пример 8.4. По данным о распределении банков по сумме выданных кредитов, приведенным в примере 8.2, определим моду графическим способом (рис. 8.2).