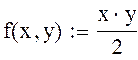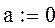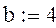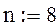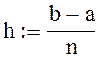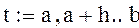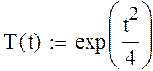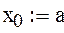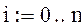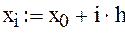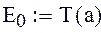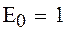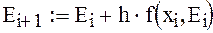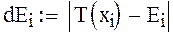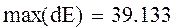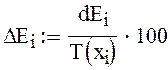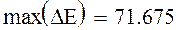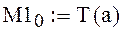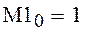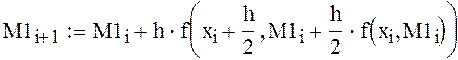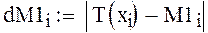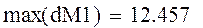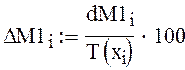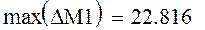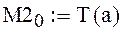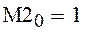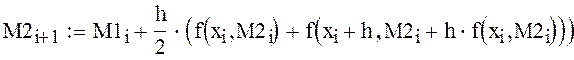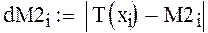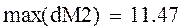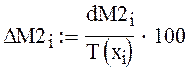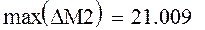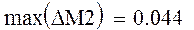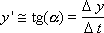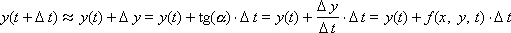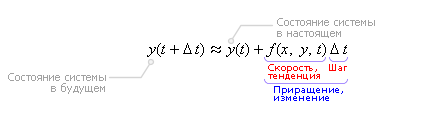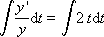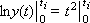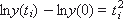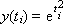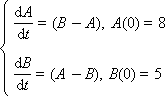как можно определить оптимальный шаг метода эйлера в вычислительных программах
На рис.10.2 точка E при х= xi+1 была бы получена методом Эйлера, в этом методе будет получена точка Ai+1.
Второй модифицированный метод Эйлера
Этот метод иногда называют методом Эйлера с пересчетом.
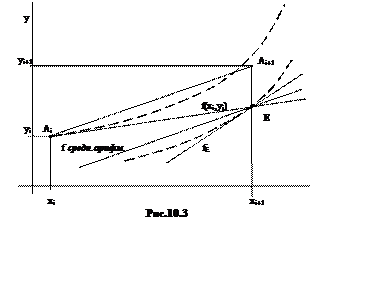
Сначала определяют значение ординаты yE в точке E как и в методе Эйлера (Рис.10.3.): yE=yi+h×f(xi, yi).
В точке E вычисляют направление проходящей через нее интегральной кривой fE=f(xi+1,yE).
по формуле 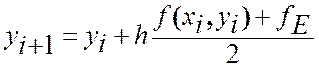
Подставив в последнюю формулу два предыдущих выражения, получим одну результирующую формулу для вычисления ординаты точки Ai+1:
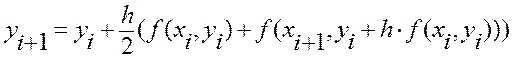
10.4 Пример выполнения работы
Точное решение данного ОДУ y(x)=exp(x 2 ∕4)
1. Вычисление общих параметров
Определяем заданную функцию
задаем границы отрезка
произвольно задаем количество интервалов
вычисляем шаг интегрирования
задаем аргумент для построения графика
точного решения ( для сравнения результатов)
функция точного решения ОДУ
начальное значение переменой x
счетчик узловых точек на отрезке [a,b]
формула определения узловых точек
Вычисляем начальное значение искомой функции
записываем формулу метода Эйлера
формула для вычислений абсолютной погрешности
вычисляем относительную погрешность в %
3. 1-й модифицированный метод Эйлера
Вычисляем начальное значение искомой функции
записываем формулу усовершенствованного метода Эйлера
формула для вычислений абсолютной погрешности
вычисляем относительную погрешность в %
4. Второй модифицированный метод Эйлера
Вычисляем начальное значение искомой функции
формула для вычислений абсолютной погрешности
вычисляем относительную погрешность в %
Полученные значения погрешностей численного решения достаточно велики.
Для уменьшения погрешности вычисления решения ОДУ необходимо изменить величину шага h. При n=2n dеличина 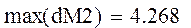
5. Построение графиков полученных решений
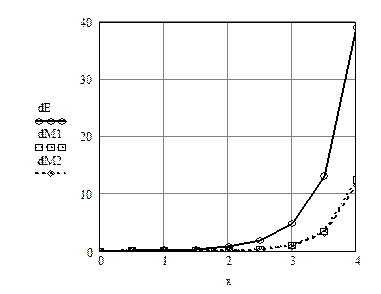
Построим графики точного и численных решений (рис.10.4) и график абсолютных погрешностей (рис.10.5)
Графики показывают, что рассматриваемые численные методы возможно применять на небольших участках интегрирования ОДУ.
Вывод: для данной функции использованные в работе численные
методы при выбранной начальной величине шага интегрирования на конце промежутка [a,b] дают большое отклонение от точного решения, поэтому необходимо шаг интегрирования выбирать значительно меньше единицы. Метод Эйлера пригоден для получения только двух или трех первых значений решения ОДУ с последующим применением других более точных численных методов.
10.5 Содержание отчета
1. Титульная страница с названием работы.
3. Назначение работы и краткие теоретические сведения.
4. Определить наименьшее число n, при котором мах(dM1) 2
Чтобы распечатать файл, скачайте его (в формате Word).
Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений
Численные методы решения задачи Коши
Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
Идея численных методов решения задачи (3), (4) состоит из четырех частей:
1. Вводится расчетная сетка по переменной \( t \) (время) из \( N_t + 1 \) точки \( t_0 \), \( t_1 \), \( \ldots \), \( t_
2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.
3. Аппроксимируем производные конечными разностями.
4. Формулируем алгоритм, который вычисляет новые значения \( \pmb
Явный метод Эйлера
При условии, что у нас известно начальное значение \( \pmb
Программная реализация явного метода Эйлера
Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом
Функция euler решения системы уравнений реализована в файле euler.py:
Неявный метод Эйлера
Для решения уравнения (8) можно использовать, например, метод Ньютона.
Программная реализация неявного метода Эйлера
Функция backward_euler решения системы уравнений реализована в файле euler.py:
Методы Рунге—Кутта
Многошаговые методы
Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен \( m+1 \).
Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет \( m \)-ый порядок.
Жесткие системы ОДУ
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование \( A \)-устойчивых или \( A(\alpha) \)-устойчивых методов.
Метод Эйлера
Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка (7) с начальным условием
Требуется найти решение уравнения (7) на отрезке [а,b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0, х1, х2,…, хn, где xi=x0+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi)»yi вычисляются последовательно по формулам уi+hf(xi, yi) (i=0,1,2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М0(х0, у0), заменяется ломаной М0М1М2… с вершинами Мi(xi, yi) (i=0,1,2,…); каждое звено МiMi+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (7), которая проходит через точку Мi. Если правая часть уравнения (7) в некотором прямоугольнике R<|x-x0|£a, |y-y0|£b>удовлетворяет условиям:
|df/dx|=|df/dx+f(df/dy)| £ M (M=const),
то имеет место следующая оценка погрешности:
где у(хn)-значение точного решения уравнения (7) при х=хn, а уn— приближенное значение, полученное на n-ом шаге.
Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. Погрешность более точного значения уn * оценивается формулой
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.
1.4 Модифицированный метод Эйлера
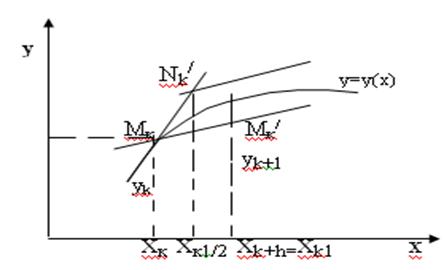
Рассмотрим дифференциальное уравнение (7) y / =f(x,y) с начальным условием y(x0)=y0. Разобьем наш участок интегрирования на n равных частей. На малом участ интегральную кривую заменим прямой линией.
Рисунок 1 Метод Эйлера в графическом виде
Получаем точку Мк(хк,ук). Через Мк проводим касательную:
(14)-рекурентные формулы метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции ук+1/2 в точках хк+1/2, затем находят значение правой части уравнения (11) в средней точке y / k+1/2=f(xk+1/2, yk+1/2) и определяют ук+1.
Для оценки погрешности в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений:
где у(х)-точное решение дифференциального уравнения.
Как можно определить оптимальный шаг метода эйлера в вычислительных программах
Variant 19 (Sukach Maxim, BS17-03)
В итоге, наше решение принимает вид:
Метод Эйлера дает возможность приближенно выразить функцию теоретически с любой наперед заданной точностью. Суть метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Метод Эйлера является методом 1-го порядка точности и называется методом ломаных.
Для вычисления используются следующие формулы:
Метод Эйлера и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1
Метод Эйлера и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1
Метод Эйлера и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1
Усовершенствованный метод Эйлера
Суть усовершенствованного метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Усовершенствованный метод Эйлера является методом 2-го порядка точности и называется модифицированным методом Эйлера.
Разница между данным методом и методом Эйлера минимальна и заключается в использовании следующих формул:
Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 9, y0 = 1, h = 0.1
Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 3, y0 = 1, h = 0.1
Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 1, y0 = 1, h = 0.1
Классический метод Рунге-Кутты
Суть метода Рунге-Кутты в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Классический метод Рунге-Кутты является методом 4-го порядка точности и называется методом Рунге-Кутты 4-го порядка точности.
Ну и как обычно, формулы:
Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1
Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1
Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1
Сравнение методов для заданной задачи
Размер ошибки всех методов на промежутке [0, 9] с шагом 0.1
Размер ошибки всех методов на промежутке [0, 3] с шагом 0.1
Размер ошибки всех методов на промежутке [0, 1] с шагом 0.1
Очевидно что, классический метод Рунге-Кутты справляется с задачей аппроксимации в случае данного уравнения намного лучше чем Метод Эйлера и Усовершенствованный метод Эйлера.
График глобальной средней ошибки
Глобальная ошибка в зависимости от размера шага H на промежутке от 0.01 до 0.91 для x0 = 1, xf = 9
Лекция 10.
Численные методы интегрирования
дифференциальных уравнений.
Метод Эйлера
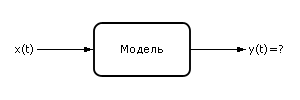
Пусть нам известна входная динамическая последовательность X (входной сигнал) и модель (способ преобразования входного сигнала в выходной сигнал). Рассматривается задача определения выходного сигнала y(t) (см. рис. 10.1 ).
| |
| Рис. 10.1. Структурная модель динамической системы с одним входом и одним выходом |
Модель динамической системы может быть представлена дифференциальным уравнением. Основное уравнение динамики:
| |
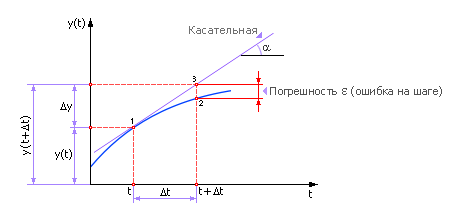
| Рис. 10.2. Иллюстрация расчета будущего состояния системы методом Эйлера на одном шаге |
|
|
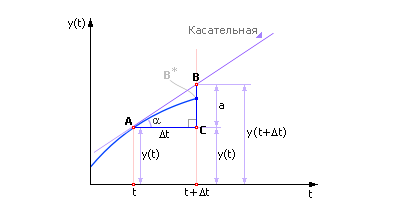
Рассмотрим еще раз это важное соотношение, выведя его из геометрических соображений ( рис. 10.3 ).
| |
| Рис. 10.3. Геометрическая иллюстрация метода Эйлера |
Пусть A точка, в которой состояние системы известно. Это «настоящее» состояние системы.
| |
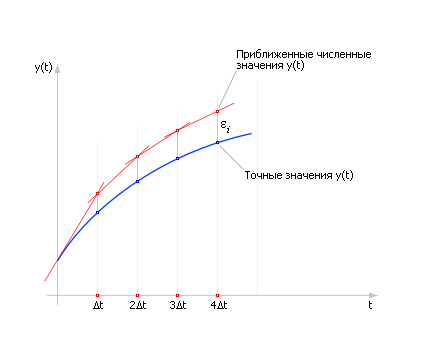
| Рис. 10.4. Нарастание суммарной ошибки в методе Эйлера на ряде шагов |
Аналитический способ решения задачи 1
Методом разделения переменных найдем:
Полученное аналитическое решение характеризуется тем, что оно является абсолютно точным, но если уравнение окажется сколько-нибудь сложным, то решение не будет найдено вовсе. Аналитический путь решения не универсален.
Численный способ решения задачи 1
Численный способ решения предполагает, что расчет будет вестись по формуле Эйлера на ряде последовательных шагов. На каждом шаге решение имеет свою ошибку (см. рис. 10.2 ), поскольку на каждом шаге кривая заменяется прямым отрезком.
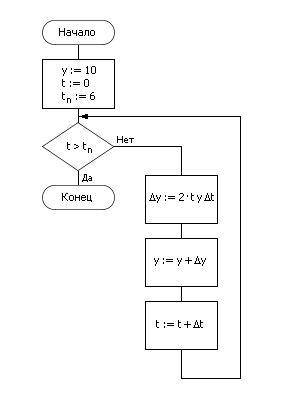
При алгоритмической реализации расчет реализуется циклом, в котором изменяется t (счетчик t ) и y :
|
| |
| Рис. 10.5. Блок-схема реализации метода Эйлера |
В реализации Стратум запись будет выглядеть так (наличие символа «
| Таблица 10.1. Численный расчет уравнения методом Эйлера и сравнение результата с точным решением на каждом шаге | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Таблица 10.2. Зависимость погрешности расчета от размера шага Δt | ||||||||||||||
|
Как видим, с уменьшением шага приращения Δt уменьшается величина относительной погрешности, а значит, повышается точность расчета.
Поскольку в методе Эйлера ошибка достаточно велика и от шага к шагу накапливается, а точность пропорциональна количеству вычислений, то метод Эйлера обычно применяют для грубых расчетов, для оценки поведения системы в принципе. Для точных количественных расчетов применяют более точные методы.
Изложенное в пп. 1-4 поясним на примере.
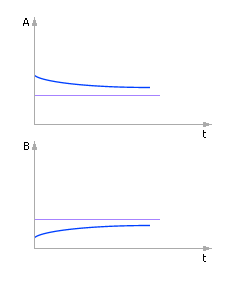
Интуитивно ясно, что при начальной разнице температур A = 8 и B = 5 температуры тел постепенно со временем должны выровняться, так как более горячее тело будет отдавать энергию более холодному, и его температура будет уменьшаться, а более холодное тело будет принимать энергию от более горячего, и его температура будет увеличиваться. Процесс теплообмена закончится (то есть изменения прекратятся) тогда, когда температуры двух тел станут одинаковыми.
Будем брать различную величину шага Δt и находить соответствующие значения A и B во времени по следующим формулам Эйлера:
Расчет при Δt = 2 (табл. 10.3).
| Таблица 10.3. Изменение температур тел при численном расчете с шагом 2 | ||||||||||||||||
|
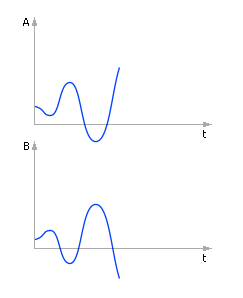
Наблюдается явление «разболтки» (см. рис. 10.6 ). Неустойчивое решение. Из физических соображений очевидно, что так вести себя два тела в процессе теплообмена не могут.
| |
| Рис. 10.6. Система ведет себя качественно неверно. Решение неустойчиво |
Расчет при Δt = 1 (табл. 10.4).
| Таблица 10.4. Изменение температур тел при численном расчете с шагом 1 | ||||||||||||||||
|
Наблюдается поведение решения системы на границе устойчивости (см. рис. 10.7 ).
| |
| Рис. 10.7. Система ведет себя качественно неверно. Решение находится на грани устойчивости |
Расчет при Δt = 0.5 (табл. 10.5).
| Таблица 10.5. Изменение температур тел при численном расчете с шагом 0.5 | ||||||||||||||||
|
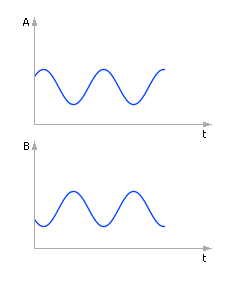
Решение устойчиво, соответствует правильной качественной картине (см. рис. 10.8 ). Температуры тел постепенно сближаются, становятся со временем одинаковыми. Но решение пока имеет большую погрешность.
| |
| Рис. 10.8. Система ведет себя качественно правильно. Решение (поведение системы) имеет большую погрешность |
Расчет при Δt = 0.1 (табл. 10.6).
| Таблица 10.6. Изменение температур тел при численном расчете с шагом 0.1 | ||||||||||||||||||||||||||||
|
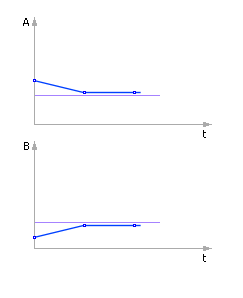
Решение устойчиво. Решение более точно (см. рис. 10.9 ).
| |
| Рис. 10.9. Система ведет себя качественно верно. Количественно решение более точно |