зачем нумеруются строки в программе для машины поста
Урок 33
Уточнение понятие алгоритма. Универсальные исполнители
§34. Уточнение понятия алгоритма
Содержание урока
Машина Поста
Машина Поста
Практически одновременно с Тьюрингом (в том же 1936 г.) и независимо от него американский математик Э. Л. Пост предложил ещё более простую систему обработки данных, на основе которой позднее была построена так называемая машина Поста.
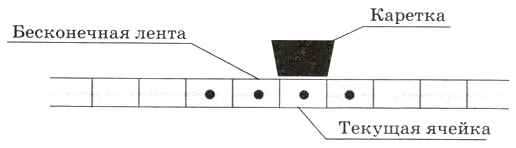
Лента в машине Поста (так же как и в машине Тьюринга) бесконечна и разбита на ячейки. Каждая ячейка может содержать метку (быть отмечена) или не содержать её (пустая ячейка) (рис. 5.6).
Таким образом, Пост сократил алфавит всего до двух цифр. Это допустимо, потому что любые данные можно перекодировать в двоичный код, сопоставив каждой букве исходного алфавита уникальную последовательность нулей и единиц.
Кроме того, алгоритм работы машины Поста задаётся не в виде таблицы, а как программа, состоящая из отдельных команд. Система команд машины Поста содержит только 6 команд:
← — переместить каретку на 1 ячейку влево;
→ — переместить каретку на 1 ячейку вправо;
0 — стереть метку в рабочей ячейке (записать 0);
1 — поставить метку в рабочей ячейке (записать 1);
? n0, n1 — если в рабочей ячейке нет метки, перейти к строке n0, иначе перейти к строке n1;
стоп — остановить машину.
Попытка стереть метку там, где её нет, или поставить метку повторно считается ошибкой, и машина аварийно останавливается.
Все строки в программе нумеруются по порядку, это необходимо для работы команды ветвления (? n0, n1). С помощью этой команды можно также строить циклы как с предусловием, так и с постусловием. Например, следующая программа перемещает каретку влево до первой отмеченной ячейки:
Если после выполнения команды ←, →, 0 или 1 требуется перейти не на следующую строку, а на какую-то другую, то номер этой строки можно записать в конце команды. Например, команда
означает «переместить каретку влево и перейти на строку 3».
При работе с машиной Поста числа обычно записывают в унарной (единичной) системе счисления, в виде непрерывной цепочки меток нужной длины (вспомните счётные палочки в младшей школе). Например, на ленте, показанной на рис. 5.6, записано число 4.
Пост предположил, что любой алгоритм может быть записан как программа для предложенного им исполнителя. В теории алгоритмов доказано, что машины Поста и Тьюринга одинаковы по своим возможностям. Это значит, что круг задач, который они решают, тоже одинаков.
Следующая страница 
Cкачать материалы урока
Программирование на машине Поста
Недавно на хабре появилось сразу два материала, посвященных языкам из «большой четверки тьюринговых трясин»: про алгоритм Маркова и Brainfuck. Думаю, для полноты картины будет интересно сравнить эти эзотерические системы с еще одним важным алгоритмическим примитивом — машиной Поста, которой я как раз занимаюсь.
Машина Поста (wiki; для простоты оттуда же взят вариант синтаксиса) похожа на всем известную машину Тьюринга, однако обладает интересными особенностями. Она содержит лишь 6 команд, кроме того, в ячейки-биты памяти могут записываться лишь 2 символа (двоичное кодирование информации). «Естественно», никакой дополнительной памяти, не зря же эзотерикой зовется!
Таким образом, при программировании на машине Поста помимо необходимости совладать с оккамовским синтаксисом надо думать о том, как записать на ленте все промежуточные результаты, не потеряв по пути обратную тропинку к остаткам входных данных. Почему «остаткам»? Зачастую ввиду отсутствия дополнительной памяти приходится обрабатывать входные данные итеративно (а иногда и рекурсивно). Надеюсь, вышеизложенное убедительно доказывает, что написание привычных алгоритмов на машине Поста — неплохая разминка для мозгов и весьма увлекательное занятие.
Пример
Рассмотрим одну из кратчайших реализаций умножения двух натуральных чисел. Числа n и m записываются на ленте в единичной системе счисления, разделяются одной пустой ячейкой. Вход/выход алгоритма может быть таким (отмечено начальное положение каретки):
Идея алгоритма — краткое сложение. В каждом проходе цикла машина «откусывает» один бит от левого множителя и «копирует» самый правый имеющийся блок (сперва это второй множитель, затем — его последняя копия). Когда левый множитель «закончится», на ленте остается n блоков по m единиц. Их слияние дает искомое число n*m.
Проверить корректность алгоритма можно в уме, на листочке, либо с помощью этой программы.
Это самая короткая известная мне реализация умножения. Однако, потенциально ее можно ужать еще сильнее, если придумать, как экономно объединить процессы создания копий и их слияния в единый массив.
P. S. «Большой четверкой» называю машину Тьюрига, Поста, систему Маркова и Brainfuck — самые изучаемые тьюринговые трясины.
Машина Поста (устройство, команды и принцип работы)
Содержимое разработки

Машина Поста – это абстрактная (несуществующая реально) вычислительная машина, созданная для уточнения (формализации) понятия алгоритма. Представляет собой универсальный исполнитель, позволяющий вводить начальные данные и читать результат выполнения программы.
В 1936 г. американский математик Эмиль Пост в статье описал систему, обладающую алгоритмической простотой и способную определять, является ли та или иная задача алгоритмически разрешимой. Если задача имеет алгоритмическое решение, то она представима в форме команд для машины Поста.
Структура машины Поста:
Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на ячейки бесконечной в обе стороны ленты (также как у машины Тьюринга). Каждая ячейка ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или стереть символ в том месте, где она стоит.
Т.о., Пост сократил алфавит всего до двух цифр. Это допустимо, потому что любые данные можно перекодировать в двоичный код, сопоставив каждой букве исходного алфавита уникальную последовательность нулей и единиц.
Алгоритм работы машины Поста задается не в виде таблицы, а как программа для универсального исполнителя.
Программа состоит из конечного числа строк и использует всего 6 команд.
где N. — номер строки, J — строка на которую переходит управление далее.
Попытка стереть метку там, где ее нет, или поставить метку повторно считается ошибкой, и машина аварийно останавливается.
Для работы машины нужно задать программу и ее начальное состояние (т. е. состояние ленты и позицию каретки).
После запуска возможны варианты:
— работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);
— работа может закончиться командой Stop;
— работа никогда не закончится.
Все строки в программе нумеруются по порядку, это необходимо для работы команды ветвления (? n0,n1). С помощью этой команды можно также строить циклы, как с предусловием, так и с постусловием.
Пост предположил, что любой алгоритм может быть записан как программа для машины Поста.
В теории алгоритмов доказано, что машины Поста и Тьюринга одинаковы по своим возможностям. Это значит, что круг задач, который они решают, тоже одинаков.
После команд «←”, «→”, «0” и «1” можно указать номер строки, на которую нужно перейти сразу после выполнения этой команды. Например, команда ← 3 означает «переместить каретку влево и перейти на строку 3”.
При работе с машиной Поста числа обычно записывают в унарной (единичной) системе счисления, в виде непрерывной цепочки меток нужной длины (вспомните счетные палочки в младшей школе).
1. Напишите программу для машины Поста, которая увеличивает (уменьшает) число в единичной системе счисления на единицу. Каретка расположена слева от числа.
2. Напишите программу для машины Поста, которая складывает два числа в единичной системе счисления. Каретка расположена над пробелом, разделяющим эти числа на ленте.
Пример работы машины Поста:
Задача: увеличить число 3 на единицу (изменить значение в памяти с 3 на 4).
Целое положительное число на ленте машины Поста представимо идущими подряд метками, которых на одну больше, чем кодируемое число. Это связано с тем, что одна метка обозначает ноль, а уже две – единицу, и т.д.
Допустим, точно известно, что каретка стоит где-то слева от меток и обозревает пустую ячейку. Тогда программа увеличения числа на единицу может выглядеть так:
2.2. Алгоритмическая машина Поста
Система команд машины, включающая шесть действий
Данный перечень должен быть дополнен следующими условиями:
Еще одним исходным соображением является следующее: поскольку знаки любого конечного алфавита могут быть закодированы цифрами, преобразование исходного слова может быть представлено в виде некоторых правил обработки чисел. По этой причине в машине Поста предусматривается только запись (представление) целых положительных чисел.
Целое число k записывается на ленте машины Поста посредством k + 1 следующих подряд отмеченных секций, т.е. применяется унарная система счисления. Соседние записи чисел на ленте разделяются одной или несколькими пустыми секциями. Ниже приведен пример записи чисел 0, 2 и 3.
Рис. 2.2. Пример записи чисел 0, 2 и 3
Круг вычислительных задач, решаемых с помощью машины Поста, весьма широк. Однако как указывалось выше, на уровне элементарных шагов все сводится к постановке или удалению метки и сдвигу головки. В качестве примеров рассмотрим несколько задач, традиционно обсуждаемых при освоении машины Поста. Поскольку вид программы (последовательности команд машины) зависит от начального состояния машины, оно должно быть в явном виде указано в постановке задачи.
На ленте записано некоторое число, и головка обозревает одну из помеченных секций (любую). Составить программу прибавления единицы к этому числу. Ситуация иллюстрируется рисунком 2.3.
Рис. 2.3. Иллюстрация рассматриваемой ситуации
Программа, обеспечивающая решение задачи, состоит из 4-х команд:
На ленте записано некоторое число, и головка обозревает одну из свободных секций (любую) левее записи. Составить программу прибавления единицы к этому числу.
Комментарий к работе программы подобен приведенному выше с той лишь разницей, что метка ставится перед исходным числом.
* Машина Поста обеспечивает весьма неплохую и полезную практику программирования. Недостатком оказывается чисто теоретический (т.е. непроверяемый) характер программ, однако он достаточно легко преодолевается, если построить эмуляцию машины на каком-либо языке программирования.
Задачи по Python с решениями
Свежие записи
Машина Поста
На этом шаге мы рассмотрим машину Поста.
Абстрактные (т.е. существующие не реально, а лишь в
воображении), машины Поста и Тьюринга, предназначенные для доказательств различных утверждений о свойствах программ для них, были предложены независимо друг от друга (и практически одновременно) в 1936 г. американским математиком Эмилем Постом и английским математиком Алланом Тьюрингом. Эти машины представляют собой универсальных исполнителей являющихся полностью детерминированными, позволяющих «вводить» начальные данные, и после выполнения программ «читать» результат. Машина Поста менее популярна, хотя она значительно проще машины Тьюринга. С ее помощью можно вести обучение первым навыкам составления программ для ЭВМ. Абстрактная машина Поста представляет собой бесконечную ленту, разделенную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V», и головки, которая может перемещаться вдоль ленты на одну клетку вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, или проверять наличие в клетке метки. Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины. В каждый момент времени головка («-») находится над одной из клеток ленты и, как говорят, обозревает ее. Информация о местоположения головки вместе с состоянием ленты характеризует состояние машины Поста, рис.1.

Рис.1. Состояние машины Поста
Команда машины Поста имеет следующую структуру:
Существует всего шесть команд машины Поста, рис.2.

Рис.2. Команды машины Поста
Ситуации, в которых головка должна наносить метку там, где она уже имеется, или, наоборот, стирать метку там, где ее нет, являются аварийными (недопустимыми).
Программой для машины Поста будем называть непустой список команд, такой что:
С точки зрения свойств алгоритмов, изучаемых с помощью машины Поста, наибольший интерес представляют причины останова машины при выполнении программы:
Будем понимать под начальным состояние головки ее положение против пустой клетки левее самой левой метки на ленте.
Рассмотрим реализацию некоторых типичных элементов программ машины Поста.

Рис.3. Пример фрагмента программы машины Поста
1. Пусть задано исходное состояние головки и требуется на пустой ленте написать две метки: одну в секцию под головкой, вторую справа от нее. Это можно сделать по следующей программе (справа от команды показан результат ее выполнения, рис.3).
2. Покажем, как можно воспользоваться командой условного перехода для организации циклического процесса. Пусть на ленте имеется запись из нескольких меток подряд и головка находится над самой крайней меткой справа. Требуется перевести головку влево до первой пустой позиции.
Программа будет иметь следующий вид:

Рис.4. Программа машины Поста
Команда условного перехода является одним из основных средств организации циклических процессов, например, для нахождения первой метки справа (или слева) от головки, расположенной над пустой клеткой; нахождение слева (или справа) от головки пустой клетки, если она расположена над меткой и т.д.
3. Остановимся на представлении чисел на ленте машины Поста и выполнении операций над ними.
Число k представляется на ленте машины Поста идущими подряд k+1 метками (одна метка означает число «0»). Между двумя числами делается интервал как минимум из одной пустой секции на ленте. Например, запись чисел 3 и 5 на ленте машины Поста будет выглядеть так:

Рис.5. Запись чисел 3 и 5 на ленте машины Поста
Обратим внимание, что используемая в машине Поста система записи чисел является непозиционной.
Составим программу для прибавления к произвольному числу единицы. Предположим, что на ленте записано только одно число и головка находится над одной из клеток, в которой находится метка, принадлежащая этому числу:

Рис.6. Увеличение числа на единицу
Для решения задачи можно переместить головку влево (или вправо) до первой пустой клетки, а затем нанести метку.
Программа, добавляющая к числу метку справа, имеет вид:

Рис.7. Текст программы, добавляющей метку справа
Программа, добавляющая к числу метку слева, имеет вид:

Рис.8. Текст программы, добавляющей метку слева
Отличие только в направлении движения головки в первой команде. Проверьте работоспособность этих программ на каких-либо частных примерах.

Рис.9. Блок поиска числа

Рис.10. Тексты программ
В первом случае не нужно перемещать головку к крайней левой метке числа.
Машину Поста можно рассматривать как упрощенную модель ЭВМ. В самом деле, как ЭВМ, так и машина Поста имеют:
Обе машины работают на основе программы. Однако в машине Поста информация располагается линейно и читается подряд, а в ЭВМ можно читать информацию по адресу; набор команд ЭВМ значительно шире и выразительнее, чем команды машины Поста, и т.д.
На следующем шаге мы рассмотрим машину Тьюринга.