алгоритм преобразования двоично десятичного кода в двоичный код
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
Двоично-десятичная система счисления. Десятичные цифры от 0 до 9 заменяются представляющими их двоичными тетрадами: 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, 5=0101, 6=0110, 7=0111, 8=1000 и 9=1001. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. И тем не менее, двоично-десятичная система счисления применяется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах (в частности, «Ямаха» стандарта MSX).
Принцип построения этой системы достаточно прост: каждая десятичная цифра преобразуется прямо в свой десятичный эквивалент из 4 бит, например: 369110=0011 0110 1001 0001DEC:
Десятичное число 3 6 9 1 Двоично-десятичное число 0011 0110 1001 0001
Преобразуем двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Получим 1000 0000 0111 0010DEC = 807210:
Двоично-десятичное число 1000 0000 0111 0010 Десятичное число 8 0 7 2
Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
Преобразование двоичных чисел в двоично-десятичные
Арифметико-логическое устройство AVR-микроконтроллеров (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде. В двоичном коде считываются результаты преобразования АЦП, в двоичном коде (в формате целых чисел или чисел с плавающей точкой) удобно выполнять обработку результатов измерения. Однако, когда окончательный результат отображается на индикаторе, он должен быть преобразован в десятичный формат, удобный для восприятия человеком.
В данном разделе рассматриваются программы преобразования двоичных чисел в двоично-десятичные.
1. Форматы представления десятичных чисел
Неупакованный десятичный код является подмножеством международной таблицы кодирования символов ASCII (Таблица 1). Видно, что для хранения неупакованных десятичных чисел требуется в два раза больше памяти, так как каждая цифра представляется 8-битным кодом. Таблица 1: ASCII-коды десятичных цифр
2. Преобразование целых 16-битных чисел в двоично-десятичные числа
На сайте www.atmel.com предлагается программа «bin2bcd16» для преобразования целых 16-битных двоичных чисел в двоично-десятичные упакованные числа. В данной статье рассматривается программа «bin16bcd5» (см. Приложение, Программа 1), написанная Терешкиным А. В. согласно алгоритму, изложенному в [1], и выполняющая ту же задачу. Последняя программа по быстродействию, длине кода и количеству используемых регистров оказалась более эффективной, чем первая.
Алгоритм программы «bin16bcd5» заключается в следующем. Предположим, что имеется целое беззнаковое 16-битное число (диапазон от 0 до 65535). Очевидно, что необходимо найти 5 десятичных цифр. Способ преобразования заключается в том, чтобы, вычитая из исходного числа число 10000, сначала определить десятичную цифру десятков тысяч. Затем находится цифра тысяч последовательным вычитанием числа 1000 и т. д. Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.
Программа «bin16ASCII5» (см. Приложение, Программа 2) преобразует целое двоичное 16-битное число в десятичное неупакованное число. При этом используется тот же алгоритм.
3. Преобразование двоичной дроби в двоично-десятичную дробь
Двоичная дробь, по определению, представляется следующим выражением:
Из этого представления следует алгоритм преобразования (Рис. 2), который содержит m шагов. На каждом шаге к двоично-десятичному результату прибавляется очередная двоичная цифра и весь результат делится на 2.
На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата. Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено. Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений.
Сложить эту цифру с двоично-десятичным числом означает, что ее нужно поместить в разряд единиц двоично-десятичного числа, откуда при последующем делении на два цифра A-i сдвинется в старший разряд старшей тетрады десятичной дроби. При программировании мы можем представлять, что разрядом единиц десятичной дроби является бит переноса С.
При делении на два двоично-десятичного упакованного числа, так же как и при делении двоичного числа, его сдвигают вправо на один разряд. При этом на два делится каждая тетрада, то есть каждая десятичная цифра. При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется. При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 (вес старшего разряда тетрады). Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды.
4. Преобразование чисел с плавающей точкой в двоично-десятичные числа
Представление чисел с плавающей точкой имеет следующий вид:
Такое представление часто используется и в десятичной системе счисления для представления очень больших или очень малых чисел. Мантисса и порядок представляют собой целые знаковые числа. Знак мантиссы является знаком всего числа. Порядок показывает истинное положение точки вместо того, которое она занимает в изображении мантиссы. Двоичное число с плавающей точкой отличается от привычного нам десятичного тем, что точка является двоичной, то есть порядок показывает на количество двоичных (а не десятичных) разрядов, на которое необходимо переместить эту точку влево или вправо.
Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля. Но для двоичного числа требование того, что старшая цифра отличается от нуля означает, что эта цифра равна 1. Если старшая цифра точно известна, то ее можно не хранить в памяти.
Перевод из десятичной системы счисления в двоичную
Перед тем как перейти к алгоритму перевода, вспомним алфавит двоичной и десятичной системы счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Для перевода чисел из десятичной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления
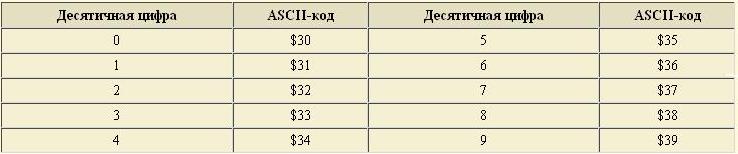
Пример 1 : перевести десятичное число 123 в двоичную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
Алгоритм перевода десятичной дроби в двоичную систему
Пример 2: перевести число 0,123 в двоичную систему.
Решение будет выглядеть следующим образом:
0.123 ∙ 2 = 0.246 (0)
0.246 ∙ 2 = 0.492 (0)
0.492 ∙ 2 = 0.984 (0)
0.984 ∙ 2 = 1.968 (1)
0.968 ∙ 2 = 1.936 (1)
0.936 ∙ 2 = 1.872 (1)
0.872 ∙ 2 = 1.744 (1)
0.744 ∙ 2 = 1.488 (1)
0.488 ∙ 2 = 0.976 (0)
0.976 ∙ 2 = 1.952 (1)
0.952 ∙ 2 = 1.904 (1)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Перевод дробного десятичного числа в двоичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
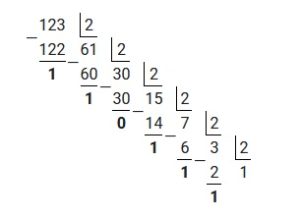
Пример 3: перевести число 110,625 из десятичной системы в двоичную
Для решения примера потребуется отдельно перевести 110 и отдельно 0,625 из десятичной системы в двоичную, используя вышеизложенные алгоритмы. Таким образом переведя 110, получим:
Перевод десятичной дроби 0,625 выглядит так:
0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)
0.5 ∙ 2 = 1 (1)
Теперь осталось соединить результаты перевода. Таким образом: 110.62510=1101110.1012
Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.
Преобразование двоичного кода в двоично-десятичный
При преобразовании четырехразрядного двоичного числа в двоично-десятичное: числа до 9 включительно остаются без изменения.
Числа свыше 9, представляющие собой псевдотетрады, подвергаются коррекции.
Двоичные числа, содержащие более 4 разрядов, можно преобразовать
аналогичным образом. Для этого двоичное число, начиная со старшего разряда, «вдвигается» справа налево в двоично-десятичную разрядную сетку, как показано на рис. 6. Когда какая-либо единица пересекает границу между двоично-десятичными разрядами, возникает ошибка. Действительно, в случае двоичного числа разрядное значение этой единицы при сдвиге увеличивается с 8 до 16, тогда как для двоично-десятичного числа оно возрастает от 8 до 10. Поэтому на этом этапе двоично-десятичное число как бы уменьшается на 6. Следовательно, для коррекции необходимо прибавлять 6 к числу во всех случаях, когда единица пересекает границу между двоично-десятичными разрядами. К числу десятков надо прибавить 6, если единица перейдет в разряд сотен, и т.д.
Составленное таким образом двоично-десятичное число имеет правильное значение, однако оно может еще содержать псевдотетрады. Чтобы этого не было, возникающие псевдотетрады корректируют непосредственно после каждого шага сдвига, прибавляя 6 к соответствующей декаде с переносом 1 в следующую.
Рис. 6. Преобразование двоичного кода в двоично-десятичный,
в качестве примера взято число 218.
Вместо того чтобы прибавлять после сдвига 6, с тем же успехом можно перед сдвигом прибавлять 3. Необходимость такой коррекции можно также определить перед сдвигом. Если значение тетрады меньше или равно 4 =- 01002, то при последующем сдвиге не произойдет перехода единицы через границу между декадами и не возникнут псевдотетрады. Таким образом, такую тетраду можно будет без изменений сдвигать влево. Если значение тетрады перед сдвигом равно 5, 6 или 7, то также не произойдет перехода единицы через границу, поскольку старший разряд равен нулю. Однако при этом возникнут псевдотетрады: десять, двенадцать, четырнадцать или одиннадцать, тринадцать, пятнадцать (в зависимости от того, будет ли в младший разряд сдвинут нуль или единица). Следовательно, в этих случаях необходима коррекция псевдотетрад путем прибавления 3 перед сдвигом.
Если значение тетрады составляет 8 или 9, необходимо корректировать переход единицы через границу между декадами. Поэтому после каждого сдвига появляются правильные тетрады 6 или 7 либо 8 или 9. При такой коррекции псевдотетрад полученное значение каждой тетрады не может быть более 9. Этим исчерпываются все возможности, и мы получим таблицу коррекции 2.
Преобразование двоичного числа в соответствующее двоично-десятичное можно реализовать, сдвигая влево двоичное число, записанное в регистре сдвига, разделенном на четырехразрядные секции. Каждая секция должна включать корректирующий элемент, который преобразует содержание регистра перед каждым последующим сдвигом в соответствии с таблицей переключений 3.
Наряду с подобным способом реализации преобразования кодов с помощью схем с памятью можно использовать комбинационные схемы, в которых операция сдвига проводится с помощью соответствующей логики. Эта схема представлена на рис. 7. Вместо сдвига числа справа налево здесь слева направо
Таблица 2.Таблица переключений корректирующею элемента
для преобразования двоичною кода в двоично-десятичный
«сдвигателя» границы двоично-десятичных разрядов, а каждая полученная тетрада корректируется в соответствии с табл. 2. Следовательно, для «сдвига» разрядной сетки с помощью комбинационной схемы на каждую декаду и каждый шаг сдвига необходимо по одному корректирующему элементу. Эта схема несколько упрощается, если исключить те корректирующие элементы, ко входам которых подключено менее трех двоичных разрядов, поскольку
в этом случае коррекция не нужна. На рис. 7 приведена комбинационная схема для преобразования 8-разрядного двоичного числа. Эту схему легко распространить на любое число разрядов. Элементы, не используемые для преобразования 8-разрядного числа, показаны пунктиром. С помощью записанных здесь чисел можно проследить за процессом преобразования кода для примера, приведенного
Корректирующие комбинационные схемы поставляются в виде программируемых изготовителем микросхем ПЗУ емкостью 32 байта. В одном корпусе размещаются три корректирующих элемента (рис. 8). Так как, согласно рис. 7, младший разряд не подается на корректирующую схему, то с помощью одной ИС можно преобразовать 6-разрядное двоичное число, а для 8-разрядного числа нужны три таких ИС.
Алгоритм преобразования двоично десятичного кода в двоичный код
В вычислительной технике существует задача преобразования двоичного числа в двоично-десятичное. Чаще всего — для последующего вывода на индикацию.
В международных терминах это преобразование обозначается как BIDEC.
Существует довольно много алгоритмов преобразования BIDEC.
Расмотрим три самых распространенных из них.
Обычно называется «плюс 3 и сдвиг».
Этот алгоритм основан на двоичном сдвиговом регистре для исходного числа и
двоично-десятичных сдвиговых регистрах для результата.
При работе алгоритма биты из двоичного регистра, начиная со старшего разряда, по одному вдвигаются в двоично-десятичный регистр, начиная с младшего разряда.
В терминах программного обеспечения, в двоичном регистре производится операция «СДВИГ ВЛЕВО ЧЕРЕЗ ПЕРЕНОС», а в двоично-десятичных регистрах,- та же операция, но для каждой декады, начиная с младшей. Далее анализируется каждая двоично-десятичная декада и если ее значение превышает 4, то к этой декаде прибавляется число 3.
После «выдвигания» последнего бита в двоично-десятичном регистре получается десятичный эквивалент двоичного числа.
Данный алгоритм чаще всего реализовывался аппаратно, еще в ту пору, когда не существовало микропроцессоров и персональных компьютеров.
И в настоящее время этот алгоритм довольно широко используется в его программной интерпретации в самых разных устройствах с выводом результатов на индикацию,- вольтметрах, термометрах, частотомерах, часах. Особенно это характерно для устройств на базе микроконтроллеров в исполнении радиолюбителей.
Блок-схема Алгоритма «плюс 3 и сдвиг»
Алгоритм «Плюс 3 и сдвиг».
Например: для преобразования данных
с АЦП 10 бит.
Другой алгоритм BIDEC похож на «деление в столбик» и по сути представляет собой разложение двоичного числа на десятичные множители.
Например, исходное двоичное число 65535 будет представлено в виде пяти десятичных тетрад как 6х10000 + 5х1000 + 5х100 + 3х10 + 5х1.
Данный алгоритм гораздо более привычен и, соответственно, более понятен, чем «плюс 3 и сдвиг». А для реализации этого алгоритма надо всего лишь находить максимальный множитель для каждой декады, начиная со старшей ( как и при «делении в столбик»).
Алгоритм «деление в столбик».
Например: для преобразования данных
с АЦП 10 бит.
Есть и другие алгоритмы BIDEC.
Среди них наиболее заметен «метод обратного счета», основанный на синхронном вычитании единицы из двоичного счетчика и прибавлении единицы к двоично-десятичному.
Этот алгоритм предельно прост и понятен, особенно специалистам по аппаратной части.
Однако, и при аппаратной и при программной реализации скорость работы у него — самая худшая из всех возможных алгоритмов.
Хотя, безусловно, в случаях, некритичных к быстродействию, этот алгоритм наиболее компактен, прост и дешев как при аппаратной, так и при программной реализации.
Алгоритм «метод обратного счета».
Например: для преобразования данных
с АЦП 10 бит.
А теперь интересно будет сравнить скорость работы алгоритмов.
Поскольку, алгоритм 3, Алгоритм обратного счета — самый медленный, остается сравнить алгоритмы 1 и 2.
Если в качестве примера взять двоичное число, состоящее из 16 бит, то после преобразования получим 5 разрядов десятичного числа.
Число команд, необходимое для преобразования, по алгоритмам выглядит так:
Для Алгоритма «плюс 3 и сдвиг»
Число десятичных разрядов для анализа — 5
Сдвигов в двоичном регистре — 16
Условных переходов в двоичном регистре — 15
Сдвигов в 10-х регистрах — 3х16 = 48
Сравнений в 10-х регистрах — 5х16 = 80
Условных переходов в 10-х регистрах — 5х16 = 80
Условных сложений «+3» — до 5х16 = 80
Итого команд от 239 (если не было ни одного +3) до 319
Для Алгоритма «деление в столбик»
Число десятичных разрядов для анализа — 5-1 = 4
Число вычитаний на каждый разряд — 9
Условных переходов на разряд — 9
Установок адреса констант на разряд — 1
Итого команд (9+9+1) х 4 = 76
Как видно из сравнения, Алгоритм «деление в столбик» как минимум в 3 раза быстрее, чем Алгоритм «плюс 3 и сдвиг».
Кроме того, при увеличении числа двоичных разрядов, время преобразования по алгоритму «плюс 3 и сдвиг» возрастает в квадрате, а в алгоритме «деление в столбик» — пропорционально. Например, если время преобразования двоичного числа 16 бит принять за единицу, то преобразование двоичного числа 32 бита займет в 4 раза больше времени в Алгоритме «плюс 3 и сдвиг» и в два раза больше времени в Алгоритме «деление в столбик».
И еще.
Алгоритм «деление в столбик» имеет интересную особенность,-
поскольку анализ начинается со старшей декады и в порядке уменьшения числа для сравнения, то чем больше исходное число, тем быстрее оно будет преобразовано.
Так например, число 9999 будет преобразовано в 9 раз быстрее, чем число 1111.
Таким образом, при программной реализации
у Алгоритма «деление в столбик» практически нет конкурентов.
Он самый быстрый и компактный. К тому же, имеет абсолютно регулярную структуру,-
все ступени преобразования одинаковы и различаются только заранее известными константами.
Преобразование двоично-десятичного кода в двоичный
Во многих случаях двоично-десятичный код можно достаточно просто получить непосредственно, например с помощью двоично-десятичных счетчиков. Как будет показано ниже, в двоично-десятичном коде также можно выполнять многие вычислительные операции. Однако в некоторых случаях необходимо все же провести преобразование его в двоичный код.
Рис. 7. Преобразование двоичного кода в двоично-десятичный
с помощью комбинационной схемы. Приведенные значения соответствуют
преобразованию числа 218.
Рис. 8. Структура интегральной микросхемы для преобразования
двоичного кода в двоично-десятичный SN 74185.
Это можно сделать путем последовательного деления числа на 2. Для этого десятичное число делится на 2. Если оно нечетное, то в остатке получится 1, т.е. в разряде 2° записывается 1. Затем частное от деления еще раз делится на 2, и, если остаток равен нулю, в разряде 2 1 записывается 0. Если остаток равен 1, то в этом разряде записывается 1. Аналогично получают и более старшие разряды двоичного числа. Деление двоично-десятичного числа на 2 очень просто можно провести путем сдвига вправо на один разряд, так как отдельные цифры уже представлены в двоичном коде. Самый правый бит, выдвинутый из двоично-десятичной разрядной сетки, и является искомым значением разряда. Но если при сдвиге единица пересекает границу между декадами, то возникает ошибка: при переходе от десятков к единицам значение разряда должно уменьшиться наполовину от десяти до пяти. Однако в случае двоичного числа эта величина становится равной восьми. Поэтому, для коррекции нужно вычесть 3. Из этого вытекает следующее правило коррекции: если старший разряд в декаде равен единице, то необходимо данную декаду уменьшить на три. Таким образом, можно непосредственно составить таблицу переключений для корректирующего элемента 3. Процесс преобразования заканчивается, если все двоично-десятичное число будет выдвинуто из разрядной сетки.
На рис. 9 приведена комбинационная схема для преобразования 272-разрядного двоично-десятичного числа. Здесь, так же как и в схеме на рис. 7, сдвиг двоично-десятичных разрядов достигается путем соответствующего соединения одинаковых комбинационных схем. Чтобы наглядно продемонстрировать структуру этой
Таблица 3.Таблица переключений корректирующего элемента
для преобразования двоично-десятичного кода в двоичный
Рис. 9. Преобразование двоично-десятичного кода в двоичный с помощью комбинационной схемы. Приведенные значения соответствуют преобразованию числа 218.
схемы, на рис. 9. изображены все три корректирующих элемента для каждой ступени кодопреобразователя. В действительности если старший разряд корректирующего элемента не используется, то, согласно табл. 3, коррекция не нужна и данный элемент можно исключить. На рис. 9 такие элементы изображены пунктирной линией.
Рис. 10. Структура интегральной микросхемы для преобразования
двоично-десятичного кода в двоичный.
Корректирующие схемы составляются из отдельных секций, содержащих по два элемента (рис. 10). Каждая секция представляет собой одну интегральную микросхему ПЗУ на 32 байта, программируемую изготовителем. Такая микросхема (типа SN 74184) имеет пять входов и пять выходов.
Литература:
1. В.В. Стрыгин «Основы вычислительной, микропроцессорной техники и программирования», стр: 64-67.
2. У. Титце, К. Шенк «Полупроводниковая схемотехника», стр: 321-325.
3. Э.В. Евреинов «Цифровая и вычислительная техника», стр: 74-76.
4. В.А. Скаржепа «Электроника и микросхемотехника» (сборник задач), стр: 122-127.
ЗАНЯТИЕ 1.1.10 Назначение сумматоров. Комбинационные сумматоры. Синтез
одноразрядного комбинационного сумматора.
ВОПРОСЫ ЗАНЯТИЯ:
1. Назначение и классификация сумматоров.
2. Комбинационные сумматоры. Синтез одноразрядного комбинационного сумматора.
ПЕРВЫЙ ВОПРОС
Сумматор – электронный узел, выполняющий операцию суммирования цифровых кодов двух чисел. При сложении двух чисел, представленных в виде двоичных кодов, происходит сложение этих чисел в данном i-м разряде и прибавление единицы переноса (если она возникает) из младшего (i—1)-го разряда.
По принятой системе счисления и кодирования различают сумматоры двоичные, троичные, десятичные, двоично-десятичные и др.
По способу организации суммирования сумматоры могут быть комбинационные и накапливающие.
Сумматор для сложения многоразрядных чисел представляет собой набор одноразрядных сумматоров, имеющих входы для слагаемых и переноса из младшего разряда и выходы суммы и переноса в старший разряд.
Рис. 1. Условное графическое Рис. 2. Условное графическое
обозначение полусумматора. обозначение одноразрядного сумматора.
По способу обработки многоразрядных чисел различают сумматоры последовательные, параллельные ипараллельно-последовательные.
Рассмотрим сложение двух целых двоичных чисел без знаков А и В с формированием их суммы S:
Из примера следует, что при формировании результата в любом i-м разряде необходимо учесть значения чисел в этом разряде аi и Ьi а также перенос в этот разряд из предыдущего разряда р.Формируются значение суммы в этом разряде si и перенос в следующий разряд pi+1. Сумматор может быть построен в виде комбинационного устройства, содержащего схемы для сложения отдельных разрядов (одноразрядные двоичные сумматоры). Условия функционирования одноразрядного двоичного сумматора определяются в табл. 1.
Булевы функции, описывающие работу одноразрядного двоичного сумматора, можно записать в виде
Используя различные варианты преобразования этих функций, можно реализовать большое число структур одноразрядных двоичных сумматоров.
ВТОРОЙ ВОПРОС
Суммирование двоичных чисел в вычислительных устройствах осуществляется комбинационными сумматорами. Одним из простейших суммирующих устройств является комбинационный одноразрядный суммирующий элемент, таблица истинности и схема которого показаны на рис. 1.
Рис.1 Таблица истинности (а) одноразрядного
комбинационного сумматора и его схема (б).
Устройство осуществляет суммирование двух одноразрядных двоичных чисел, сумма s которых также имеет один разряд. На выходе р устройства формируется сигнал переноса в следующий, более старший разряд, если оба суммируемых числа имеют единичные значения.
Нетрудно заметить, что функция s реализуется элементом неравнозначности (сумма по модулю 2):
Функция переноса — это операция «И»:
На рис. 1, б показано условное обозначение данного элемента. Этот элемент называют иногда одноразрядным полусумматором, поскольку в нем не учитывается возможность суммирования сигнала переноса из предыдущего разряда.
Два одноразрядных полусумматора образуют одноразрядный сумматор. Таблица истинности, схема и его условное обозначение показаны на рис. 2.
Рис. 2. Таблица истинности (а), схема (б) и условное
обозначение одноразрядного сумматора.
Промежуточная сумма s образуется в результате суммирования значений одноименных разрядов ai и bi исходных чисел Затем s суммируется с сигналом переноса рi-1 из предыдущего разряда и получается окончательное значение суммы si. Сигналы переносов 



Рис. 3. Схема одноразрядного комбинационного сумматора
Рис. 3. Схема многоразрядного комбинационного сумматора.
Одноразрядный накапливающий сумматор.Это логическая схема, в которой исходные слова хi, уi, pi — 1 в виде входных сигналов поступают на вход поочередно и накапливаются и сохраняются на выходе после прекращения подачи сигналов. Схема накапливающего сумматора строится на основе триггера со счетным входом, реализующим операцию сложения по модулю 2.
Схема одноразрядного накапливающего сумматора приведена на рис. 4. В этой схеме после установки триггера в состояние 0 сигналы xi,yi, pi-1 поступают на элемент И – ИЛИ последовательно в моменты времени t1, t2, t3 соответственно.
В момент времени t1 поступает сигнал первого слагаемого хi ,который запоминается в триггере. Затем в момент времени t2 через И – ИЛИ на счетный вход триггера поступает сигнал второго слагаемого уi. При этом триггер реализует функцию si = fi(xi 
Сигнал переноса в старший разряд имеет две составляющие,
одна из которых вырабатывается схемой И1; peaлизующей переключательную функцию.Вторая составляющая вырабатывается в том случае, если хi и yi равны 1. Она реализуется схемой И2, на один из входов которой подается сигнал с инверсного выхода триггера, а на другой второе слагаемое yi,которое подается в дискретный момент времени t3. В этот момент времени в триггере хранится функция fi, поэтому элемент И2 реализует переключательную функцию
Таким образом, сигнал переноса на выходе схемы ИЛИ3 определяется выражением
Рис. 4. Схема одноразрядного накапливающего сумматора.
Основной недостаток накапливающего сумматора – малое быстродействие, поскольку в каждом цикле суммирования одного разряда двух слагаемых число срабатываний счетной схемы может быть равно трем.
Литература:
1. В.В. Стрыгин «Основы вычислительной, микропроцессорной техники и программирования» стр: 105-108.
2. Б.Я. Лихтциндер «Микропроцессоры и вычислительные устройства в радиотехнике» стр: 43-44.
ЗАНЯТИЕ 1.1.11 Комбинационные сумматоры последовательного и
ЗАНЯТИЕ 1.1.12 Основные характеристики надежности цифровых устройств.
Функции систем контроля и диагностирования.
ВОПРОСЫ ЗАНЯТИЯ:
1. Сумматоры последовательного и параллельного действия.
2. Основные характеристики надежности цифровых устройств.
3. Функции систем контроля и диагностирования.
ПЕРВЫЙ ВОПРОС
Последовательные сумматоры. Это одноразрядные сумматоры, в которых числа поступают на сложение последовательным кодом. Они преобразуют последовательные коды слагаемых, подаваемых на вход сумматора, в последовательный код суммы этих слагаемых.
Рис. 1. Схема параллельного n-разрядного сумматора.
Быстродействие такого сумматора определяется временем суммирования в разряде сумматора tc и временем распространения переноса tp последовательно по всему n-разрядному сумматору, т. е. T=tc+(n—l)tp.
Для повышения быстродействия сумматоры выполняют с использованием схем с ускоренным распространением переносов (параллельным или групповым).
Для сложения n-разрядных чисел необходимо п – 1 одноразрядных полных сумматоров и один полусумматор в нулевом разряде (рис. 1, г).
В настоящее время в виде микросхем выпускаются одно-(165ИМ1), двух- (155ИМ2) и четырехразрядные (155ИМЗ, 564ИМ1) двоичные сумматоры. На рис 2, а показано условное графическое обозначение четырехразрядного двоичного сумматора. Входы At и В;, где t = 1, 2, 3, 4 и Ро логически равноценны.
ВТОРОЙ ВОПРОС
Под надёжностью изделия (элемента, узла, устройства, системы) понимают свойство последнего сохранять своё качество при определенных условиях эксплуатации в течении заданного промежутка времени, т.е. надежность – качество, развернутое во времени.
Изделия в процессе эксплуатации подразделяются по показателям надежности:
1. Невосстанавливаемые изделия – изделия, поведение которых существенно лишь до первого отказа. Характеризуются следующими показателями надёжности: интенсивностью отказов λ(t); частотой отказов f(t); вероятностью безотказной работы P(t); вероятностью отказа Q(t); наработкой на отказ То.
2. Восстанавливаемые изделия – изделия, эксплуатация которых допускает их многократный ремонт. Характеризуются следующими количественными показателями надежности: параметрами потока отказов ω(t) и потока восстановлений μ(t); функцией готовности Кг(t); коэффициентом готовности Кг; средним временем работы между двумя отказами tср; средним временем восстановления tв.
При анализе и сравнении качества изделий, при расчете надежности, при определении вероятности исправного действия системы и сроков ремонта, при определении запасов комплектующих изделий, а также при некоторых других технических и экономических расчетах необходима количественная оценка надежности.
Для удобства рассмотрения показатели надежности подразделяются на четыре группы.