фильтр согласованный с кодом баркера

Согласованная фильтрация типовых широкополосных сигналов

Изготовление аналоговых согласованных фильтров, особенно для сложных энергоёмких сигналов, сложно и не допускает перестройки их параметров. Поэтому компьютерное моделирование, в частности в пакете прикладных программ MATLAB, позволяет изучать особенности согласованной обработки сигналов и реакцию согласованного фильтра на входное воздействие.

В публикации рассматривается опыт создания и использования програмных продуктов в среде MATLAB при проведении занятий с обучающимися по дисциплине «Радиотехнические системы».

Оптимальная временная обработка сигнала, принимаемого на фоне стационарного белого шума, сводится к вычислению корреляционного интеграла. Это выражение аналогично интегралу свёртки, который описывает реакцию линейного фильтра с импульсной характеристикой на принимаемый сигнал. Эта аналогия позволяет использовать для вычисления корреляционного интеграла линейный фильтр, импульсная характеристика которого согласована с ожидаемым сигналом. При приёме сигнала на фоне стационарного белого шума импульсная характеристика согласованного фильтра (СФ) зеркальна по отношению к ожидаемому сигналу. Согласованный фильтр является оптимальным устройством обработки входной реализации с точки зрения получения максимального отношения сигнал-шум.

Изготовление аналоговых согласованных фильтров, особенно для сложных энергоёмких сигналов, сложно и не допускает перестройки их параметров. Поэтому компьютерное моделирование, в частности в пакете прикладных программ MATLAB, позволяет изучать особенности согласованной обработки сигналов и реакцию согласованного фильтра на входное воздействие.

Рис.1. Структурная схема оптималного обнаружителя сигнала со случайными параметрами

Практическое занятие «Согласованная фильтрация типовых широкополосных сигналов» учебной дисциплины «Радиотехнические системы» проводится методом решения задач по оценке выходного эффекта при прохождении ЛЧМ и ФКМ радиоимпульса через устройства оптимальной обработки с помощью программ.

Для обеспечения данного вида занятия были разработаны программы в ППП MATLAB с простым пользовательским интерфейсом (UI) (рис.2.).

Рис.2. Окно среды GUIDE

Ниже приведена ссылка.

Дальнейшая компиляция продукта осуществляется с помощью встроеных приложений (рис.3).

Рис.3. Окно компилятора Matlab

При отработке первого вопроса занятия используется программа «Имитационная модель исследования согласованной обработки ЛЧМ сигналов».

Рис.4. Свидетельство о государственной регистрации программ для ЭВМ

Рис.5. Внешний вид окна программы «Имитационная модель исследования согласованной обработки ЛЧМ сигналов»

При рассмотрении первого вопроса особое внимание уделяется выработке у обучающихся практических умений в расчете коэффициента сжатия ЛЧМ сигнала на выходе устройства оптимальной обработки и оценке систематической ошибки измерения времени запаздывания.

В развернувшемся рабочем окне в поле «Зондирующий сигнал» вводятся параметры зондирующего сигнала. Для обработки сигнала с заданными параметрами необходимо нажать кнопку «Расчет» (рис.6).

Рис.6. К пояснению порядка работы в окне программы

После нажатия кнопки «Расчет» запускается процесс моделирования прохождения сигнала с заданными параметрами через согласованный фильтр.

Рис.7. К пояснению эффекта сжатия сигнала и процесса измерения информативного параметра сигнала

Определение ошибки измерения времени запаздывания находится как разность между истинным временем запаздывания, которое соответствует случаю нулевой частотной расстройки и измеренным значением.

При отработке первого вопроса занятия используется программа «Имитационная модель исследования согласованной обработки ФКМ сигналов, манипулированных по коду Баркера».

Рис.8. Свидетельство о государственной регистрации программ для ЭВМ

В ходе отработки второго вопроса занятия уделяется внимание обучающихся на форму ФКМ сигнала и величину уровня боковых лепестков на выходе устройства оптимальной обработки.

1. В развернувшемся рабочем окне во вкладке «Зондирующий сигнал» во всплывающем списке необходимо выбрать код Баркера входного (исследуемого) сигнала.

Рис.9. Внешний вид окна программы «Имитационная модель исследования согласованной обработки ФКМ сигналов,манипулированных по коду Баркера»

2. В окне «Значение кода импульсной характеристики» задается код импульсной характеристики согласованного фильтра.

Рис.10. К пояснению порядка работы в окне программы

3. После нажатия кнопки «Расчёт» запускается моделирование процесса прохождения сигнала через фильтровое устройство оптимальной обработки (рис.1). Полученные реализации входного сигнала, импульсной характеристики фильтра и сигнала на выходе СФ обучающиеся зарисовывают в рабочих тетрадях.

Рис.7. К пояснению процесса обработки ФКМ сигнала

4. Рассчитается коэффициент сжатия.

5. Оценивается отношение амплитуды боковых лепестков АКФ по отношению к главному.

6. В окне «Значение кода импульсной характеристики» задается значение, отличное от кода Баркера (в любом из дискрет импульсной характеристики меняется код на обратный). После процесса моделирования по графикам оценивается изменение временной структуры сигнала на выходе фильтра. Рассчитывается значение коэффициента сжатия.

7. Сравниваются значения коэффициентов сжатия, рассчитанных в пунктах 4 и 6.

8. Определяются ошибки измерения времени запаздывания при несогласованной обработке сигнала.

Источник

Повсеместное распространение беспроводных сетей, развитие инфраструктуры хот-спотов, появление мобильных технологий со встроенным беспроводным решением (Intel Centrino) привело к тому, что конечные пользователи (не говоря уже о корпоративных клиентах) стали обращать все большее внимание на беспроводные решения. Такие решения рассматриваются, прежде всего, как средство развертывания мобильных и стационарных беспроводных локальных сетей и средство оперативного доступа в Интернет. Однако конечный пользователь, не являющийся сетевым администратором, как правило, не слишком хорошо разбирается в сетевых технологиях, поэтому ему трудно сделать выбор при покупке беспроводного решения, особенно учитывая многообразие предлагаемых сегодня продуктов. Бурное развитие технологии беспроводной связи привело к тому, что пользователи, не успев привыкнуть к одному стандарту, вынуждены переходить на другой, предлагающий еще более высокие скорости передачи. Речь, конечно же, идет о семействе протоколов беспроводной связи, известном как IEEE 802.11, куда входят следующие протоколы: 802.11, 802.11b, 802.11b+, 802.11a, 802.11g. В последнее время стали говорить и о расширении протокола 802.11g.

Будущее стандарта 802.11a довольно туманно. Наверняка в России и в Европе этот стандарт не получит широкого распространения, да и в США, где он сейчас используется, скорее всего, в ближайшее время произойдет переход на альтернативные стандарты. А вот новый стандарт 802.11g имеет значительные шансы завоевать признание во всем мире. Другое преимущество нового стандарта 802.11g заключается в том, что он полностью совместим со стандартами 802.11b и 802.11b+, то есть любое устройство, поддерживающее стандарт 802.11g, будет работать (правда, на меньших скоростях соединения) и в сетях стандарта 802.11b/b+, а устройство, поддерживающее стандарт 802.11b/b+ — в сетях стандарта 802.11g, хотя и с меньшей скоростью соединения.

Совместимость стандартов 802.11g и 802.11b/b+ обусловлена, во-первых, тем, что они предполагают использование одного и того же частотного диапазона, а во-вторых, что все режимы, предусмотренные в протоколах 802.11b/b+, реализованы и в стандарте 802.11g. Поэтому стандарт 802.11b/b+ можно рассматривать как подмножество стандарта 802.11g.

Физический уровень протокола 802.11

Обзор протоколов семейства 802.11b/g целесообразно начат именно с протокола 802.11, который, хотя уже и не встречается в чистом виде, в то же время является прародителем всех остальных протоколов. В стандарте 802.11, как и во всех остальных стандартах данного семейства, предусмотрено использование частотного диапазона от 2400 до 2483,5 МГц, то есть частотный диапазон шириной 83,5 МГц, который, как будет показано далее, разбит на несколько частотных подканалов.

Технология уширения спектра

В основе всех беспроводных протоколов семейства 802.11 лежит технология уширения спектра (Spread Spectrum, SS). Данная технология подразумевает, что первоначально узкополосный (в смысле ширины спектра) полезный информационный сигнал при передаче преобразуется таким образом, что его спектр оказывается значительно шире спектра первоначального сигнала. То есть спектр сигнала как бы «размазывается» по частотному диапазону. Одновременно с уширением спектра сигнала происходит и перераспределение спектральной энергетической плотности сигнала — энергия сигнала также «размазывается» по спектру. В результате максимальная мощность преобразованного сигнала оказывается значительно ниже мощности исходного сигнала. При этом уровень полезного информационного сигнала может в буквальном смысле сравниваться с уровнем естественного шума. В результате сигнал становится в каком то смысле «невидимым» — он просто теряется на уровне естественного шума.

Собственно, именно в изменении спектральной энергетической плотности сигнала и заключается идея уширения спектра. Дело в том, что если подходить к проблеме передачи данных традиционным способом, то есть так, как это делается в радиоэфире, где каждой радиостанции отводится свой диапазон вещания, то мы неизбежно столкнемся с проблемой, что в ограниченном радиодиапазоне, предназначенном для совместного использования, невозможно «уместить» всех желающих. Поэтому необходимо найти такой способ передачи информации, при котором пользователи могли бы сосуществовать в одном частотном диапазоне и при этом не мешать друг другу. Именно эту задачу и решает технология уширения спектра.

Существует несколько различных технологий уширения спектра, однако для дальнейшего понимания протокола 802.11 нам необходимо детально познакомиться лишь с технологией уширения спектра методом прямой последовательности (Direct Sequence Spread Spectrum, DSSS).

Технология DSSS

При потенциальном кодировании информационные биты — логические нули и единицы — передаются прямоугольными импульсами напряжений. Прямоугольный импульс длительности T имеет спектр, ширина которого обратно пропорциональна длительности импульса. Поэтому чем меньше длительность информационного бита, тем больший спектр занимает такой сигнал.

Для преднамеренного уширения спектра первоначально узкополосного сигнала в технологии DSSS в каждый передаваемый информационный бит (логический 0 или 1) в буквальном смысле встраивается последовательность так называемых чипов. Если информационные биты — логические нули или единицы — при потенциальном кодировании информации можно представить в виде последовательности прямоугольных импульсов, то каждый отдельный чип — это тоже прямоугольный импульс, но его длительность в несколько раз меньше длительности информационного бита. Последовательность чипов представляет собой последовательность прямоугольных импульсов, то есть нулей и единиц, однако эти нули и единицы не являются информационными. Поскольку длительность одного чипа в n раз меньше длительности информационного бита, то и ширина спектра преобразованного сигнала будет в n-раз больше ширины спектра первоначального сигнала. При этом и амплитуда передаваемого сигнала уменьшится в n раз.

Чиповые последовательности, встраиваемые в информационные биты, называют шумоподобными кодами (PN-последовательности), что подчеркивает то обстоятельство, что результирующий сигнал становится шумоподобным и его трудно отличить от естественного шума.

Как уширить спектр сигнала и сделать его неотличимым от естественного шума, понятно. Для этого, в принципе, можно воспользоваться произвольной (случайной) чиповой последовательностью. Однако, возникает вопрос: а как такой сигнал принимать? Ведь если он становится шумоподобным, то выделить из него полезный информационный сигнал не так то просто, если вообще возможно. Оказывается, возможно, но для этого нужно соответствующим образом подобрать чиповую последовательность. Используемые для уширения спектра сигнала чиповые последовательности должны удовлетворять определенным требованиям автокорреляции. Под термином автокорреляции в математике подразумевают степень подобия функции самой себе в различные моменты времени. Если подобрать такую чиповую последовательность, для которой функция автокорреляции будет иметь резко выраженный пик лишь для одного момента времени, то такой информационный сигнал возможно будет выделить на уровне шума. Для этого в приемнике полученный сигнал умножается на ту же чиповую последовательность, то есть вычисляется автокорреляционная функция сигнала. В результате сигнал становится опять узкополосным, поэтому его фильтруют в узкой полосе частот и любая помеха, попадающая в полосу исходного широкополосного сигнала, после умножения на чиповую последовательность, наоборот, становится широкополосной и обрезается фильтрами, а в узкую информационную полосу попадает лишь часть помехи, по мощности значительно меньшая, чем помеха, действующая на входе приемника (рис. 1).

Рис. 1. Использование технологии уширения спектра позволяет предавать данные на уровне естественного шума.

Источник

Свойства согласованных фильтров

1. Импульсная характеристика СФ является «зеркальным отражением» сигнала, с которым он согласован, относительно момента времени 0,5t₀ (с точностью до постоянного коэффициента)

.

Это свойство было положено в основу определения СФ (6.15).

2. Передаточная функция СФ

.

.

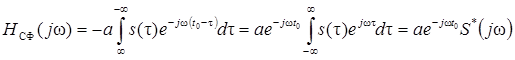
Таким образом, передаточная функция СФ с точностью до множителя совпадает с сопряженной спектральной функцией сигнала, с которым он согласован

.

Амплитудно-частотная характеристика СФ

с точностью до коэффициента а повторяет амплитудный спектр сигнала, с которым он согласован

Фазо-частотная характеристика СФ

отличается знаком от фазового спектра сигнала, с которым он согласован (без учета слагаемого –ωt₀).

3. Форма отклика СФ на «свой» сигнал (сигнал с которым он согласован)

.

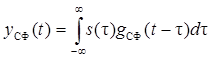
Учитывая, что из (6.15) вытекает , получим

.

Таким образом, отклик СФ на «свой» сигнал с точностью до коэффициента совпадает с его корреляционной функцией, смещенной по оси времени на интервал t₀ (рис. 6.7)

.

Из полученного результата вытекают следующие выводы:

· Отклик СФ на «свой» сигнал с точностью до постоянного коэффициента совпадает с его корреляционной функцией.

· Длительность отклика на «свой» сигнал всегда равна 2Т.

· СФ не восстанавливает форму сигнала, искаженного шумом. Его задача создать один отсчет y(t₀), по которому можно наилучшим образом судить о присутствии на входе «своего» сигнала.

4. СФ обеспечивает наибольшее отношение сигнал/шум (с/ш) на своем выходе при действии на входе аддитивной смеси «своего» сигнала и центрированного нормального белого шума 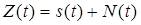со спектральной плотностью мощности N=N_О/2.

Докажем это, уточнив предварительно, что под отношением с/ш на выходе СФ понимают отношение математического ожидания отсчета случайной реакции СФ Y(t) в момент времени t₀ = T к корню из ее дисперсии

. (6.16)

Рассмотрим произвольный линейный фильтр с передаточной функцией . Поскольку представляет собой отсчет реакции y_s(T) на математическое ожидание воздействия, каковым является сигнал s(t), то

.

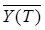
Полученное выражение представляет собой не что иное, как скалярное произведение двух векторов в комплексном пространстве Гильберта, если иметь в виду следующие соответствия:

.

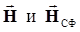
Вычислим дисперсию случайной величины

Подставляя полученные результаты в выражение (6.16) и применяя неравенство Коши-Буняковского-Шварца

,

.

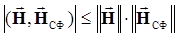
Наибольшее значение с/ш (равенство в полученном выражении) достигается при совпадении векторов , т. е. для случая использования СФ, что и требовалось доказать. Это чрезвычайно важное свойство некоторые авторы закладывают в основу определения СФ.

Найдем саму величину отношения с/ш на выходе СФ при действии на его входе «своего» сигнала

, (6.17)

где Е – энергия «своего» сигнала,

N_О – односторонняя спектральная плотность мощности шума,

.

Таким образом, максимальное отношение с/ш на выходе СФ определяется энергией «своего» сигнала, независимо от его формы.

Определим отношение с/ш по мощности

,

где F_K – ширина полосы пропускания канала.

При совпадении ширины полосы пропускания канала с шириной спектра сигнала F_K = F_s имеем

.

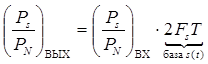
Отсюда вытекает целесообразность выбора сигналов с большой базой 2F_sT для передачи дискретных сообщений, что позволяет увеличить отношение с/ш при согласованной фильтрации.

Согласованная фильтрация и корреляционный прием

Некоторых типичных сигналов

Рассмотрим особенности когерентного приема некоторых сигналов и реализации соответствующих согласованных фильтров.

Прямоугольные видеоимпульсы

Сигнал в виде прямоугольного видеоимпульса s(t) (рис. 6.8,а) и импульсная характеристика g_СФ(t) согласованного с ним фильтра (рис. 6.8,б) описываются выражениями

Вычислим передаточную функцию СФ

.

Сомножитель представляет собой передаточную функцию интегратора, вычитаемое в скобках – передаточная функция элемента задержки на время Т, а сама скобка соответствует алгебраическому сумматору. В итоге приходим к схеме СФ, показанной на рис. 6.9.

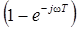
Реакция СФ на прямоугольный импульс показана на рис. 6.8,в. Для сравнения на рис. 6.8,г показана реакция на тот же сигнал коррелятора (рис. 6.10).

Прямоугольные радиоимпульсы

Сигнал в виде прямоугольного радиоимпульса s(t) описывается выражением

Импульсная характеристика g_СФ(t) согласованного с ним фильтра на интервале

.

Такого рода импульсной характеристикой обладает колебательный контур с добротностью Q ® ¥, однако, у него она продолжается во времени неограниченно. Для «гашения» импульсной характеристики (реакции контура на воздействие d(t)) в момент t=T можно воспользоваться соответствующей коммутацией контура (рис. 6.11,а) или вычитанием самой задержанной на T реакции (рис. 6.11,б).

Прямоугольные радиоимпульсы и реакции на них СФ и коррелятора можно видеть на рис. 6.12, 6.19, 6.20 и 6.21.

Сложные двоичные сигналы

Рассмотрим сигналы в виде n-последовательностей импульсов прямоугольной формы положительной и отрицательной полярности с фиксированным размахом. Возможный вид такого сигнала при n = 7 показан на рис. 6.13,а. Усложнение сигнала объясняется желанием получить определенную (острую) форму отклика на выходе согласованного с ним фильтра и повысить отношение с/ш. Поскольку , то ясно – чем острее (короче) , тем шире спектр сигнала и больше его база. Сигналы такого рода удобно использовать в радиолокационных и в асинхронно адресных телекоммуникационных системах.

Проанализируем импульсную характеристику ТФ со стороны входа А, как его реакцию на воздействие в виде d-функции. Поданная этот вход d-функция (рис. 6.15,а) появится на отводах ЛЗ с соответствующими задержками и после суммирования в сумматоре (с учетом полярности) создаст последовательность, показанную на рис. 6.15,б. На выходе СФ_П, согласованного с одиночным П-импульсом длительностью , каждая из этих d-функций вызовет реакцию (по определению – импульсную характеристику) в виде самого этого импульса. В результате получим на выходе ТФ n-последовательность, изображенную на рис. 6.15,в, т.е. рассмотренная схема работает как формирователь сложного двоичного сигнала (рис.6.14,а). Интересно, что при подаче d-функции на вход Б на выходе ТФ получим реакцию (смотри графики на рис. 6.15,г и 6.15,д), совпадающую с показанной на рис. 6.13,б. Таким образом, один и тот же ТФ можно использовать в качестве формирователя сложного двоичного сигнала (вход А) и в качестве согласованного с этим сигналом фильтра (вход Б).

Из двоичных n-последовательностей наибольший интерес представляют собой последовательности (коды) Баркера. Они обладают важным свойством

,

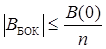
где В_БОК – величина боковых лепестков корреляционной функции,

В(0) – начальное значение корреляционной функции.

Показанная на рис. 6.14 двоичная последовательность как раз и является кодом Баркера при n = 7. Импульсную характеристику и реакцию фильтра, согласованного с семиэлементным кодом Баркера, на этот «свой» сигнал (смещенную на Т корреляционную функцию кода Баркера) можно видеть на рис. 6.22.

Произвольные F-финитные сигналы

Согласно теореме Котельникова сигналы с ограниченным частотой F спектром точно передаются последовательностью своих отсчетов, взятых через интервалы и, следовательно, могут быть заменены ступенчатой функцией (рис. 6.16,а), которая отличается от двоичного сигнала (рис. 6.13,а) только размахами отдельных П-импульсов длительностью . Отсюда вытекает возможность формирования такого рода сигналов и их согласованной фильтрации с помощью аналогового трансверсального фильтра (рис. 6.17, 6.24). Его схема отличается от схемы двоичного ТФ (рис. 6.14) только заменой фильтра, согласованного с П-ипульсом (СФ_П) на сглаживающий фильтр (ФНЧ с частотой верхнего среза F) и использованием в цепях отводов ЛЗ усилителей с коэффициентами усиления, пропорциональным отсчетам F-финитного сигнала.

Источник