как построить граф по коду
Алгоритм построения кода Прюфера по дереву
Вход: дерево с n вершинами.
Выход: код Прюфера длины n – 2.
Повторить n – 2 раза
Выбрать вершину v – лист дерева с наименьшим номером;
Добавить номер единственного соседа v в последовательность кода Прюфера;
Удалить вершину v из дерева;
Пример 1. Построение всех кодов Прюфера длины 2. Для этого следует рассмотреть все возможные деревья из 4 вершин. Под каждым деревом приведен соответствующий код.
Алгоритм составления дерева по коду:
1.Выписываем висячие вершины, всего вершин на 2 больше чем значений в коде дерева.
2. находим наименьшее натуральное число, которое не встречается в последовательности.
3. это число – номер вершины, которую необходимо соединить с вершиной, которая встречается первой в коде.
4. находим следующее число.
Рассмотрим применение данного алгоритма на примере.
Пример 1. Постройте дерево, которому соответствует код
1. Выписываем висячие вершины. Всего вершин на 2 больше чем значений в коде дерева, в данном случае такими будут 3,4,5,6,7.
2. Вершину с минимальным номером (3) соединяем с первым значением кода (1).
Дальше вершины (2) больше нет в коде, потому она становится висячей с наименьшим номером, потому следующим шагом я соединяю ее (2) со следующим значением кода (1).
Далее 6 – 7. Код закончился, осталась 6. Соединяем ее с 1.
Задана матрица инцидентности неориентированного графа G:
Работа с графами онлайн
Визуализация графа, поиск кратчайшего пути и многое другое. В разделе Справка вы найдете обучающие видео.
Создание алгоритмы
Поддержите наш проект: сбор средств добавления новых алгоритмов.
Ваш алгоритм отправлен на модерацию и в случае успеха он будет добавлен на сайт.
Выделите и перемещайте объекты или перемещайте рабочую область.
Перемещайте курсор для перемещения объекта
Выделите и перемещайте объекты или перемещайте рабочую область.
Перемещайте курсор для перемещения объекта
Кликните на рабочую область, чтобы добавить вершину. Нумерация вершин
Выделите первую вершину для создания дуги
Выделите вторую вершину, которую хотите соединить
Выделите вершину, из которой хотите найти кратчайших путь
Выделите конечную вершину кратчайшего пути
Расстояние между вершинами %d
Пути не существует
Кликните по объекту, который хотите удалить
Число компонентов связности графа равно
Число слабо связных компонентов равно
Что вы думаете о сайте?
Имя (email для ответа)
Матрица имеет неправильный формат
Сохранение изображения графа
Граф не содержит Эйлеров цикл
Граф содержит Эйлеров цикл
Граф не содержит Эйлерову цепь
Граф содержит Эйлерову цепь
Граф минимальных расстояний.
Нажмите для сохранения
Показать матрицу расстояний
Выделите исток максимального потока
Выделите сток максимального потока
Максимальный поток из %2 в %3 равен %1
Поток из %1 в %2 не существует
Граф не содержит Гамильтонов цикл
Граф содержит Гамильтонов цикл
Граф не содержит Гамильтонову цепь
Граф содержит Гамильтонову цепь
Выбирете начальную вершину обхода
Стиль отрисовки вершины
Стиль отрисовки дуги
Мультиграф не поддерживает все алгоритмы
Выделите несколько объектов используя Cmd⌘.
Выделите несколько объектов используя Ctrl.
Найти компоненты связности
Найти Эйлеров цикл
Найти Эйлерову цепь
Алгоритм Флойда — Уоршелла
Найти Гамильтонов цикл
Найти Гамильтонову цепь
Поиск максимального потока
Поиск минимального остовного дерева
Визуализация на основе весов
Поиск радиуса и диаметра графа
Поиск кратчайший путь алгоритмом Дейкстры
Рассчитать степень вершин
Вес минимального остовного дерева равен
Мы игнорировали ориентацию дуг при рассчете.
Граф не является связным
Выделите первый граф для проверки на изоморфизм. Кликните по любой вершине графа
Выделите второй граф для проверки на изоморфизм. Кликните по любой вершине графа
Выделите граф, которому должны быть изоморфны подграфов. Кликните по любой вершине графа
Выделите граф в котором необходимо найти изоморфные подграфы. Кликните по любой вершине графа
Графы не изоморфны
Количество изоморфных подграфов равно
Граф не содержит изоморфных подграфов
Поиск изоморфных подграфов
Для использования алгоритма необходимо создать хотя бы 2 не связных графа
Проверка изоморфности графов
Стиль обычной дуги
Стиль выделенной дуги
Стиль обычной вершины
Стиль выделенной вершины
Код Прюфера
Деревья. Кратко напомним
Дерево – частный случай графа. Деревья широко применяются в программировании. Дерево – это связный граф без циклов. Дерево называется помеченным, если каждой вершине соответствует уникальная метка. Обычно это число.
Определение. Построение кода Прюфера для заданного дерева
Код Прюфера – это способ взаимно однозначного кодирования помеченных деревьев с n вершинами с помощью последовательности n-2 целых чисел в отрезке [1,n]. То есть, можно сказать, что код Прюфера – это биекция между всеми остовными деревьями полного графа и числовыми последовательностями.
Данный способ кодирования деревьев был предложен немецким математиком Хайнцом Прюфером в 1918 году.
Рассмотрим алгоритм построения кода Прюфера для заданного дерева с n вершинами.
На вход подается список ребер. Выбирается лист дерева с наименьшим номером, затем он удаляется из дерева, и к коду Прюфера добавляется номер вершины, которая была связана с этим листом. Эта процедура повторяется n-2 раза. В конце концов, в дереве останется только 2 вершины, и алгоритм на этом завершается. Номера оставшихся двух вершин в код не записываются.
Таким образом, код Прюфера для заданного дерева – это последовательность из n-2 чисел, где каждое число – номер вершины, связанной с наименьшим на тот момент листом – то есть это число в отрезке [1,n].
Пример 
Исходное дерево 
Код Прюфера: 1 
Код Прюфера: 1 5 
Код Прюфера: 1 5 2 
Код Прюфера: 1 5 2 6 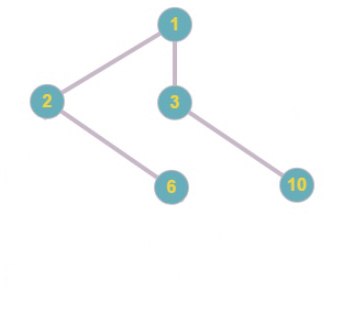
Код Прюфера: 1 5 2 6 6 
Код Прюфера: 1 5 2 6 6 2 
Код Прюфера: 1 5 2 6 6 2 1 
Код Прюфера: 1 5 2 6 6 2 1 3
Восстановление дерева по его коду Прюфера
Рядом с задачей построения кода Прюфера стоит задача восстановления закодированного дерева. Будем рассматривать алгоритм восстановления дерева со следующими условиями: на вход подается последовательность цифр (вершин), которая представляет код Прюфера, результатом будет список ребер дерева. Таким образом, задача будет решена.
Рассмотрим алгоритм декодирования подробно. Помимо кода нам нужен список всех вершин графа. Мы знаем, что код Прюфера состоит из n-2 вершин, где n – это число вершин в графе. То есть, мы можем по размеру кода определить число вершин в закодированном дереве.
В результате, в начале работы алгоритма мы имеем массив из кода Прюфера размера n-2 и массив всех вершин графа: [1… n]. Далее n-2 раза повторяется такая процедура: берется первый элемент массива, содержащего код Прюфера, и в массиве с вершинами дерева производится поиск наименьшей вершины, не содержащейся в массиве с кодом. Найденная вершина и текущий элемент массива с кодом Прюфера составляют ребро дерева. Данные вершины удаляются из соответствующих массивов, и описанная выше процедура повторяется, пока в массиве с кодом не закончатся элементы. В конце работы алгоритма в массиве с вершинами графа останется две вершины, они составляют последнее ребро дерева. В результате получаем список всех ребер графа, который был закодирован.
Пример
Восстановим дерево по коду Прюфера, который был получен в примере кодирования.
Первый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 4
Список ребер: 1 4
Второй шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 7
Список ребер: 1 4, 5 7
Третий шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 5
Список ребер: 1 4, 5 7, 2 5
Четвертый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 8
Список ребер: 1 4, 5 7, 2 5, 6 8
Пятый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 9
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9
Шестой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 6
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6
Седьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 2
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2
Восьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1
Завершение алгоритма
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1, 3 10
Заключение
Код Прюфера был предложен как наглядное и простое доказательство формулы Кэли о числе помеченных деревьев. На практике же его используют чаще для решения комбинаторных задач.
Построение графов для чайников: пошаговый гайд
Ранее мы публиковали пост, где с помощью графов проводили анализ сообществ в Точках кипения из разных городов России. Теперь хотим рассказать, как строить такие графы и проводить их анализ.
Под катом — пошаговая инструкция для тех, кто давно хотел разобраться с визуализацией графов и ждал подходящего случая.
1. Выбор гипотезы
Если попытаться визуализировать хотя бы что-то, бездумно загрузив данные в программу построения графов, результат вас не порадует. Поэтому сначала сформулируйте для себя, что хотите узнать с помощью графов, и придумайте жизнеспособную гипотезу.
Для этого разберитесь, какие данные у вас уже есть, что из них можно представить «объектами», а что – «связями» между ними. Обычно объектов значительно меньше, чем связей — можно таким образом проверять себя.
Наш тестовый пример мы готовили совместно с командой Точки кипения из Томска. Соответственно, все данные для анализа по мероприятиям и их участникам у нас будут именно оттуда. Нам стало интересно, сформировалось ли из участников этих мероприятий сообщество и как оно выглядит с точки зрения принадлежности участников к бизнесу, университетам и власти.
Мы предположили, что люди, которые посетили одно и то же мероприятие, связаны друг с другом. Причем чем чаще они присутствовали на мероприятиях совместно, тем сильнее связь.
Во втором случае мы решили узнать, как соотносится принадлежность участников к одному из «нетов» (наших ключевых направлений) с интересующими их сквозными технологиями. Равномерно ли распределение, есть ли «горячие темы»? Для этого анализа мы взяли данные по участникам мероприятий из 200 томских технологических компаний.
В принципе, даже таких первичных формулировок гипотез достаточно, чтобы перейти ко второму шагу.
2. Подготовка данных
Теперь, когда вы определились с тем, что хотите узнать, возьмите весь массив данных, посмотрите, какая информация об «объектах» хранится, выкиньте все лишнее и добавьте недостающее. Если данные распределены по нескольким источникам, предварительно соберите все в одну кучу, убрав дубли.
Поясню на примере. У нас были данные об участниках 650 мероприятий. Это, условно говоря, 650 эксель-таблиц с
23000 записей в них, содержащих поля «Leader ID», «Должность», «Организация». Для постройки графа достаточно одного уникального идентификатора (тут, к счастью, такой есть – это Leader ID) и признака, привязывающего каждого участника к одной из трех рассматриваемых сфер: власти, бизнесу или университетам. И этой информации у нас еще нет.
Чтобы получить ее, можно пойти напролом: в каждом из 650 файлов убрать лишние столбцы и добавить новое поле, заполнить его значениями для каждой строки, например: «1» для власти, «2» для бизнеса и «3» для образования и науки. А можно сначала объединить все 650 файлов в один большой список, убрать дубли и только после этого добавлять новые значения. В первом случае такая работа займет 1-2 месяца. Во втором — 1-2 недели.
Вообще при добавлении новых атрибутов старайтесь предварительно группировать данные. Например, можно отсортировать участников по компаниям/организациям и скопом выставлять признак.
Готовим данные дальше. Для их загрузки в большинство программ визуализации потребуется создать два файла: один — с перечнем вершин, второй — со списком ребер.
Файл вершин в нашем случае содержал два столбца: Id — номер вершины и Label — тип. Файл ребер содержал также два столбца: Source — id начальной вершины, Target — id конечной вершины.
Как превратить данные о том, что участники 1, 2, 5 и 23 посетили одно мероприятие, в ребра? Необходимо создать шесть строк и отметить связь каждого участника с каждым: 1 и 2, 1 и 5, 1 и 23, 2 и 5, 2 и 23, 5 и 23.
Во втором нашем примере таблицы выглядели так:
В качестве вершин перечислены как рынки, так и сквозные технологии. Если, скажем, представитель компании, относящейся к рынку «Технет» (ID=4), посетил мероприятие по теме «Большие данные и ИИ» (ID=17), в таблицу ребер заносим ребро (строку), соединяющее эти вершины (Source=4, Target=17).
Этап подготовки данных – это самая трудоемкая часть процесса, но наберитесь терпения.
3. Визуализация графа
Итак, таблицы с данными подготовлены, можно искать средство для их представления в виде графа. Для визуализации мы использовали программу Gephi — мощный опенсорсный инструмент, способный обрабатывать графы с сотнями тысяч вершин и связей. Скачать его можно с официального сайта.
Скриншоты я буду делать со второго проекта, в котором было небольшое число вершин и связей, чтобы все было максимально понятно.
Первым делом нам надо загрузить таблицы с вершинами и ребрами. Для этого выбираем пункт «Импортировать из CSV» из меню раздела «Лаборатория данных».
Сначала грузим файл с вершинами. На первом экране формы указываем, что импортируем именно вершины, и проверяем, чтобы программа правильно определила кодировку подписей.
На третьей форме «Отчет об импорте» важно указать тип графа. У нас он не ориентирован.
Похожим образом грузим ребра. В первом окне указываем, что это файл с ребрами, и также проверяем кодировку.
Важный момент ждет нас в третьем окне «Отчет об импорте». Тут важно указать не только то, что граф не ориентирован, но и подгрузить ребра в то же рабочее пространство, что и вершины. Поэтому выбираем пункт «Append to existing workplace».
В результате перед нами предстанет граф примерно вот в таком виде (закладка «Обработка»):
Итак, ребра имеют разную толщину в зависимости от количества связей между вершинами. Посмотреть, какой вес стал у каждого ребра, можно на закладке «Лаборатория данных» в свойствах ребер в столбце Weight.
Что здесь плохо: все вершины имеют один размер и расположены абсолютно произвольно. На закладке «Обработка» мы это исправим. Сначала в верхнем левом окне выбираем Nodes и жмем на пиктограммку с кругами («Размер»). Далее выбираем пункт Ranking — он позволяет задать размер вершины в зависимости от какого-либо параметра. У нас есть возможность выбрать только один параметр — Degree (степень), который показывает, сколько ребер выходят из вершины. Выбираем минимальный и максимальный размер кружочка и жмем кнопку «Применить». Здесь же, если выбрать другие пиктограммки, можно настроить цвет маркера вершины и цвет ребер. Теперь граф уже более нагляден.
Следующее, что нужно сделать, — распутать граф. Это можно сделать вручную, двигая вершины, а можно использовать алгоритмы укладки, которые реализованы в Gephi.
Чего мы добиваемся правильной укладкой? Максимальной наглядности. Чем меньше на графе наложений вершин и ребер, чем меньше пересечений ребер, тем лучше. Также неплохо было бы, чтобы смежные вершины были расположены поближе друг к другу, а несмежные —подальше друг от друга. Ну и все было распределено по видимой области, а не сжато в одну кучу.
Как это сделать в Gephi? Левое нижнее окно «Укладка» содержит самые популярные алгоритмы укладки, построенные на силовых аналогиях. Представьте, что вершины — это заряженные шарики, который отталкиваются друг от друга, но при этом некоторые скреплены чем-то, похожим на пружинки. Если задать соответствующие силы и «отпустить» граф, вершины разбегутся на максимально допустимые пружинками расстояния.
Наиболее равномерную картину дает алгоритм Фрюхтермана и Рейнгольда. Выберите Fruchterman Reingold из выпадающего меню и задайте размер области построения. Нажмите кнопку «Исполнить». Получится что-то вроде этого:
Можно помочь алгоритму и, не останавливая его, поперетаскивать некоторые вершины, стараясь распутать граф. Но помните, что здесь нет кнопки «Отменить», вернуться к прежнему расположению вершин уже не удастся. Поэтому сохраняйте новые версии проекта перед каждым рискованным изменением.
Еще один полезный алгоритм — Force Atlas 2. Он представляет граф в виде металлических колец, связанных между собой пружинами. Деформированные пружины приводят систему в движение, она колеблется и в конце концов принимает устойчивое положение. Этот алгоритм хорош для визуализаций, подчеркивающих структуру группы и выделяющих подмножества с высокой степенью взаимодействия.
Этот алгоритм имеет большое количество настроек. Рассмотрим наиболее важные. «Запрет перекрытия» запрещает вершинам перекрывать друг друга. Разреженность увеличивает расстояние между вершинами, делая граф более читаемым. Также более воздушным граф делает уменьшение влияния весов ребер на взаимное расположение вершин.
Поигравшись с настройками, получим такой граф:
Получив граф в том виде, который вас устраивает, переходите к финальной обработке. Это закладка «Просмотр». Здесь мы можем задать, например, отрисовку графа кривыми ребрами, которая минимизирует наложение вершин на чужие ребра. Можем включить подписи вершин, задав размер и цвет шрифта. Наконец, поменять фон подложки. Например, так:
Для того чтобы сохранить получившийся рисунок, нажмите на надпись «Экспорт SVG/PDF/PNG в левом нижнем углу окна. Также отдельно не забудьте сохранить сам проект через верхнее меню «Файл» — «Сохранить проект».
В нашем случае принципиально было выделить взаимосвязь сквозных технологий с рынками НТИ, для чего мы вручную выстроили все рынки в одну линию в центре и разместили все остальное сверху и снизу. Получился вот такой граф. Все-таки для решения конкретных задач без ручной расстановки вершин обойтись не удалось.
Вы, наверное, думаете, как нам удалось раскрасить вершины в разный цвет? Есть одна хитрость. Можно перейти в закладку «Лаборатория данных», создать там новый столбец в вершинах, назвав его «Market». И заполнить для каждой вершины значениями: 1 если это рынок НТИ, 0 — если сквозная технология. Затем достаточно перейти в «Обработку», выбрать пиктограммку в виде палитры, Nodes — Partition, а в качестве разделителя — наш новый атрибут Market.
Для более сложных построений, когда требуется выделить кластеры и закрасить их разными цветами, в Gephi используется богатый арсенал статистических расчетов, результаты которых можно использовать для раздельной окраски. Находятся эти расчеты в правом столбце вкладки «Обработка».
Например, нажав кнопку «Запуск» возле расчета «Модулярность», вы узнаете оценку уровня кластеризации вашего графа. Если после этого выставить цвет вершин в зависимости от Modularity Class, появится симпатичная картинка наподобие такой:
Если вы хотите еще больше узнать о возможностях Gephi, стоит почитать руководство по работе с программой от Мартина Гранджина http://www.martingrandjean.ch/gephi-introduction/.
4. Анализ результата
Итак, вы получили итоговую визуализацию графа. Что она вам дает? Во-первых, это красиво, ее можно вставить в презентацию, показать знакомым или сделать заставкой на рабочем столе. Во-вторых, по ней вы можете понять, насколько сложной и многокластерной структурой является рассматриваемая вами предметная область. В-третьих, обратите внимание на самые крупные вершины и на самые жирные связи. Это особенные элементы, на которых все держится.
Так, построив граф экспертного сообщества, посещающего мероприятия в Точке кипения, мы сразу обнаружили участников, которые с наибольшей вероятностью выполняют роль суперконнекторов. Они являлись «вершинами», через которые кластеры объединялись в единое целое. А во втором случае мы увидели, как выглядит концентрация специалистов из томских компаний с точки зрения их принадлежности к рынку и сквозной цифровой технологии, на которую они делают ставку. Это косвенно говорит об уровне технологических компетенций и экспертизы региона.
Помощь графов в понимании окружающей действительности реально велика, так что не поленитесь и попробуйте создать собственную визуализацию данных. Это совсем не сложно, но порой трудозатратно.


