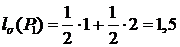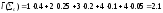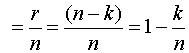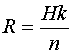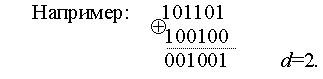коды с минимальной избыточностью

Тема: Кодирование с минимальной избыточностью.

1. Постановка задачи.

2. Описание алгоритма кодирования с минимальной избыточностью.

Постановка задачи.

На практике важно, чтобы коды сообщений имели по возможности наименьшую длину. Алфавитное кодирование пригодно для любых сообщений, если же про множество всех слов алфавита А ничего не известно, то точно сформулировать задачу оптимизации трудно. Однако на практике часто доступна дополнительная информация. Например, для сообщений, представленных на естественном языке, такой дополнительной информацией может быть распределение вероятности появления букв в сообщении. Тогда задача построения оптимального кода приобретает точную математическую формулировку и строгое решение.

Пусть задана некоторая разделимая схема алфавитного кодирования:

.

,

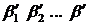
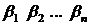
где упорядоченный набор есть перестановка упорядоченного набора , также будет разделимой. В таком случае, если длины элементарных кодов равны, то их перестановка в схеме не влияет на длину закодированного сообщения. В том случае, если длины элементарных кодов различны, то длина кода сообщения напрямую зависит и от того, какие элементарные коды каким буквам поставлены в соответствие, и от того, каков состав букв в сообщении.

Если заданы конкретное сообщение и конкретная схема кодирования, то можно подобрать такую перестановку кодов, при которой длина кода сообщения будет минимальной.

Описание алгоритма кодирования с минимальной избыточностью

Алгоритм назначения элементарных кодов, при котором длина кода фиксированного сообщения S будет минимальна при фиксированной схеме s:

− отсортировать буквы в порядке убывания количества вхождений;

− отсортировать элементарные коды в порядке возрастания длины;

− поставить коды в соответствие буквам в установленном порядке.

Пусть задан алфавит:

и вероятности появления букв в сообщении:

где р_i – вероятность появления буквы a_i, причем буквы с нулевой вероятностью появления в сообщении исключены и буквы упорядочены по убыванию вероятности их появления:

Для разделимой схемы:

алфавитного кодирования при распределении вероятностей Р существует так называемая средняя цена, или длина кодирования, – это математическое ожидание длины закодированного сообщения, которая обозначается l_s и определяется как:

Для разделимойсхемы алфавитного кодирования:

при распределении вероятностей:

цена кодирования составляет:

а при распределении вероятностей:

цена кодирования составляет:

Лекция 5.

Дата добавления: 2018-05-12 ; просмотров: 486 ; Мы поможем в написании вашей работы!

Источник

39. Коды с минимальной избыточностью (коды Хаффмана), метод построения.

Пусть р₁, р₂,…, р_r– частоты (вероятности), с которыми буквы алфавитавстречаются в исходных сообщениях. Частоты неотрицательны и удовлетворяют равенству.

Определение. Избыточностью схемы алфавитного кодирования Σ с длинами кодовых словl₁,l₂,…,l_r при заданных частотах р₁, р₂,…, р_rназывается число.

Избыточность схемы согласно определению равна .

Пример 1. При заданных частотах р₁= 0.4, р₂= 0.25, р₃= 0.2, р₄= 0.15 сравнить избыточность двух схем Σ₁и Σ₂, где

Заметим, что Σ₁– равномерная схема, а Σ₂– префиксная, поэтому обе эти схемы однозначно декодируемы. В схеме Σ₁длины кодовых словl₁ =l₂ =l₃ =l₄= 2, следовательно, её избыточность равна.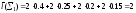

В схеме Σ₂длины кодовых словl₁ = 1,l₂ = 2,l₃ =l₄= 3, поэтому её избыточность равна.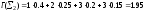

Пример 2. Для набора частот р₁ = 0.4, р₂ = 0.25, р₃ = 0.2, р₄ = 0.1, р₅ = 0.05 требуется построить суффиксный код Хафмана с исходным алфавитоми кодирующим алфавитом.

Прежде всего, по данному набору частот найдем длины кодовых слов кода Хафмана. Для этого запишем в столбец исходные частоты в порядке их убывания сверху вниз и будем преобразовывать этот столбец, на каждом шаге заменяя две самых маленьких частоты их суммой и располагая в новом столбце полученные частоты в порядке убывания. Процесс преобразования частот завершится, как только мы придем к столбцу с двумя частотами (их сумма равна единице). В таблице показаны столбцы, которые получаются в данном примере. Клетки, выделенные темным цветом, содержат сумму двух самых маленьких частот из предыдущего столбца.

Теперь построим бинарное дерево, корень которого располагается в самом верхнем ярусе. Каждая вершина, кроме корня, помечается числом из таблицы. Построение дерева и расстановка пометок его вершин выполняется рекурсивно. Сначала к единственной вершине – корню дерева – добавляются две смежные с ней вершины, которые помечаются числами из последнего столбца таблицы..

Однако по условию задачи требовалось построить суффиксную схему кодирования. Она легко получается «зеркальным отражением» префиксной схемы Σ_п.Следовательно, искомый суффиксный код Хафмана задается схемой Σ_с, где.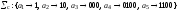

Избыточность построенного кода равна

40. Линейные коды, порождающая матрица, двойственный код.

Определение. Коды с кодирующим алфавитом В = <0,1>называются двоичными кодами.

Определение. Булева функция f (x₁,x₂,…,x_n) называется характеристической функцией двоичного кода, если она обращается в единицу на тех и только тех наборах, которые являются кодовыми словами этого кода.

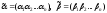
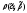
Утверждение.Пусть− два кодовых слова двоичного кода Σ. Черезобозначается расстояние Хэмминга между двумя кодовыми словамии, которое вычисляется по формуле. Формула означает, что расстояние Хэмминга между двумя кодовыми словами равно числу позиций, в которых эти слова различаются.

Определение. Кодовым расстоянием двоичного кода называется минимальное расстояние Хэмминга между двумя его кодовыми словами. Кодовое расстояние схемы Σ – это минимальное число позиций, в которых могут отличаться два её кодовых слова. Геометрическая интерпретация кодового расстояния − это длина кратчайшей цепи, которая соединяет две вершины n-мерного единичного куба, отвечающие кодовым словам данной схемы.

Утверждение.Говорят, что кодовые словалинейно зависимы, если хотя бы одно из них является линейной комбинацией остальных слов из этого набора. Если же ни одно из них не является линейной комбинацией остальных слов, то они считаются линейно независимыми.

Определение. Двоичный код называется линейным кодом, если любая линейная комбинация его кодовых слов также является кодовым словом этого кода.

Из определения линейного кода можно получить следующие его свойства:

Любой линейный код содержит нулевое кодовое слово, т.е. слово, состоящее только из нулей.

Кодовые слова линейного кода обязательно линейно зависимы, так как линейный код всегда содержит нулевое слово, а оно выражается через другие кодовые слова с помощью линейной комбинации вида .

Если линейный код не состоит из одного только нулевого слова, то можно так выбрать несколько его линейно независимых кодовых слов, чтобы все кодовые слова являлись линейными комбинациями выбранных слов.

Кодовое расстояние линейного кода равно минимальному числу единиц в ненулевом кодовом слове этого кода.

Определение. Порождающей матрицей линейного кода размерности r с длинами кодовых слов, равными n, называется матрица размера r на n, в строках которой стоят базисные кодовые слова этого кода.

Определение. Кодовые слова иназываютсяортогональными, если. Каждое слово ортогонально нулевому слову. Кроме того, оно может быть ортогонально и самому себе. Например, слово (0101) ортогонально словам (0000), (0010), (1000), (1010), (0101), (0111), (1101) и (1111). Обратим внимание на то, что эти восемь слов образуют линейный код.

Источник

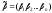
Электронные средства сбора, обработки и отображения информации

Оглавление

Помехоустойчивое кодирование

Понятие корректирующего кода

Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Клодом Шенноном. Он сформулировал теорему для дискретного канала с шумом: при любой скорости передачи двоичных символов, меньшей, чем пропускная способность канала, существует такой код, при котором вероятность ошибочного декодирования будет сколь угодно мала.

Построение такого кода достигается ценой введения избыточности. То есть, применяя для передачи информации код, у которого используются не все возможные комбинации, а только некоторые из них, можно повысить помехоустойчивость приема. Такие коды называют избыточными или корректирующими. Корректирующие свойства избыточных кодов зависят от правил построения этих кодов и параметров кода (длительности символов, числа разрядов, избыточности и др.).

В настоящее время наибольшее внимание уделяется двоичным равномерным корректирующим кодам. Они обладают хорошими корректирующими свойствами и их реализация сравнительно проста.

Наиболее часто применяются блоковые коды. При использовании блоковых кодов цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга, то есть каждой букве сообщения соответствует блок из п символов.

Блоковый код называется равномерным, если п (значность) остается одинаковой для всех букв сообщения.

Различают разделимые и неразделимые блоковые коды.

При кодировании разделимыми кодами кодовые операции состоят из двух разделяющихся частей: информационной и проверочной. Информационные и проверочные разряды во всех кодовых комбинациях разделимого кода занимают одни и те же позиции.

При кодировании неразделимыми кодами разделить символы выходной последовательности на информационные и проверочные невозможно.

Непрерывными называются такие коды, в которых введение избыточных символов в кодируемую последовательность информационных символов осуществляется непрерывно, без разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.

Общие принципы использования избыточности

Способность кода обнаруживать и исправлять ошибки обусловлена наличием избыточных символов. На ввод кодирующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из п двоичных символов, причем n>k. Всего может быть различных входных последовательностей и различных выходных последовательностей. Из общего числа выходных последовательностей только последовательностей соответствуют входным. Будем называть их разрешенными кодовыми комбинациями. Остальные ( — ) возможных выходных последовательностей для передачи не используются. Их будем называть запрещенными кодовыми комбинациями.

— случаев безошибочной передачи;

— ·(-1) случаев перевода в другие разрешенные комбинации, что соответствует необнаруживаемым ошибкам;

— ·( — ) случаев перехода в неразрешенные комбинации, которые могут быть обнаружены.

Часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи соответствует:

К_обн .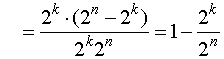

Рассмотрим, например, обнаруживающую способность кода, каждая комбинация которого содержит всего один избыточный символ (п=k+1). Общее число выходных последовательностей составит , то есть вдвое больше общего числа кодируемых входных последовательностей. За подмножество разрешенных кодовых комбинаций можно принять, например, подмножество комбинаций, содержащих четное число единиц (или нулей). При кодировании к каждой последовательности из k информационных символов добавляется один символ (0 или 1), такой, чтобы число единиц в кодовой комбинации было четным. Искажение любого четного числа символов переводит разрешенную кодовую комбинацию в подмножество запрещенных комбинаций, что обнаруживается на приемной стороне по нечетности числа единиц. Часть обнаруженных ошибок составляет:

К_обн .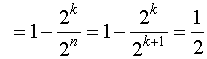

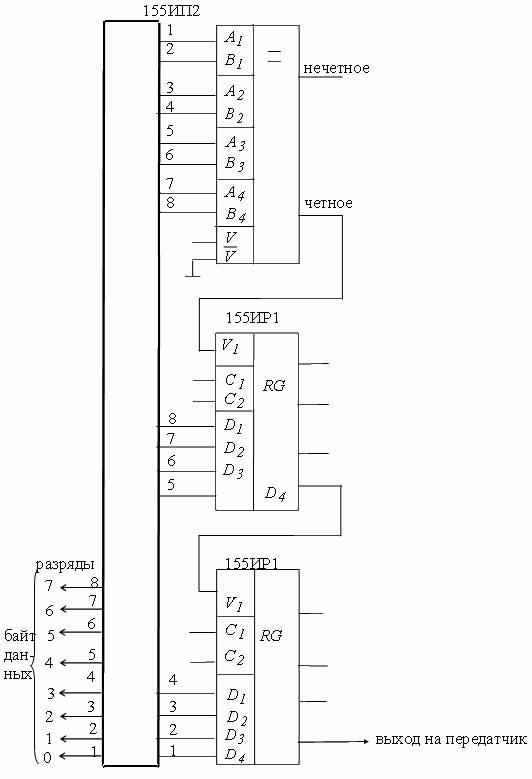
Пример кодирующего устройства с проверкой на четность показан на рис.

Основные параметры корректирующих кодов

Основными параметрами, характеризующими корректирующие свойства кодов являются избыточность кода, кодовое расстояние, число обнаруживаемых или исправленных ошибок.

Рассмотрим суть этих параметров.

Избыточность корректирующего кода может быть абсолютной и относительной. Под абсолютной избыточностью понимают число вводимых дополнительных разрядов

Относительной избыточностью корректирующего кода называют величину

_отн

_отн.

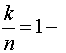
Эта величина показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы. Ее еще называют относительной скоростью передачи информации.

Если производительность источника равна Н символов в секунду, то скорость передачи после кодирования этой информации будет равна

поскольку в последовательности из п символов только k информационных.

Если число ошибок, которое нужно обнаружить или исправить, значительно, необходимо иметь код с большим числом проверочных символов. Скорость передачи информации при этом будет уменьшена, так как появляется временная задержка информации. Она тем больше, чем сложнее кодирование.

Кодовое расстояние характеризует cтепень различия любых двух кодовых комбинаций. Оно выражается числом символов, которыми комбинации отличаются одна от другой.

Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2.

Кодовое расстояние может быть различным. Так, в первичном натуральном безызбыточном коде это расстояние для различных комбинаций может различаться от единицы до п, равной значности кода.

Число обнаруживаемых ошибок определяется минимальным расстоянием между кодовыми комбинациями. Это расстояние называется хэмминговым.

В безызбыточном коде все комбинации являются разрешенными, =1. Достаточно только исказиться одному символу, и будет ошибка в сообщении.

Теорема. Чтобы код обладал свойствами обнаруживать одиночные ошибки, необходимо ввести избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными комбинациями не менее двух.

Доказательство. Возьмем значность кода п=3. Возможные комбинации натурального кода образуют следующее множество: 000, 001, 010, 011, 100, 101, 110, 111. Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Ошибки здесь не обнаруживаются и не исправляются, так как =1. Если =2, то ни одна из разрешенных кодовых комбинаций при одиночной ошибке не переходит в другую разрешенную комбинацию.

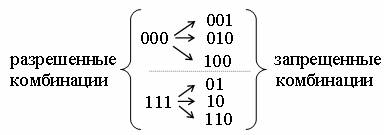
Пусть подмножество разрешенных комбинаций образовано по принципу четности числа единиц. Тогда подмножества разрешенных и запрещенных комбинаций будут такие:

Очевидно, что искажение помехой одного разряда (одиночная ошибка) приводит к переходу комбинации в подмножество запрещенных комбинаций. То есть этот код обнаруживает все одиночные ошибки.

В общем случае при необходимости обнаруживать ошибки кратности — минимальное хэммингово расстояние должно быть, по крайней мере, на единицу больше , то есть

+1.

В этом случае никакая ошибка кратности не в состоянии перевести одну разрешенную комбинацию в другую.

Ошибки можно не только обнаруживать, но и исправлять.

Теорема. Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстояние должно быть не менее трех.

Доказательство. Пусть, как и в предыдущем примере, п=3. Примем разрешенные комбинации 000 и 111 (кодовое расстояние между ними равно 3). Разрешенной комбинации 000 поставим в соответствие подмножество запрещенных комбинаций 001, 010, 100. Эти запрещенные комбинации образуются в результате возникновения единичной ошибки в комбинации 000.

Аналогично разрешенной комбинации 111 необходимо поставить в соответствие подмножество запрещенных комбинаций 110, 011, 101. Если сопоставить эти подмножества запрещенных комбинаций, то очевидно, что они не пересекаются:

В общем случае исправляемые ошибки кратности связаны с кодовым расстоянием соотношением

=2+1. (2.1)

где — сочетание из п элементов по t (число возможных ошибок кратности t на длине п-разрядной комбинации).

Если, например, п=7, =1, то из (2.1)

Нужно отметить, что каждый конкретный корректирующий код не гарантирует исправления любой комбинации ошибок. Коды предназначены для исправления комбинаций ошибок, наиболее вероятных для заданного канала связи.

Групповой код с проверкой на четность

Недостатком кода с четным числом единиц является необнаружение четных групповых ошибок. Этого недостатка лишены коды с проверкой на четность, где комбинации разбиваются на части, из них формируется матрица, состоящая из некоторого числа строк и столбцов:

Строки образуются последовательно по мере поступления символов исходного кода. Затем после формирования т строк матрицы производится проверка на четность ее столбцов и образуются контрольные символы . Контрольные символы образуются путем суммирования по модулю 2 информационных символов, расположенных в столбце:

.

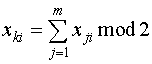
При таком кодировании четные групповые ошибки обнаруживаются. Не обнаруживаются лишь такие ошибки, при которых искажено четное число символов в столбце.

Можно повысить обнаруживающую способность кода путем одновременной проверки на четность по столбцам и строкам или столбцам и диагоналям (поперечная и диагональная проверка).

Если проверка проводится по строкам и столбцам, то код называется матричным.

Проверочные символы располагаются следующим образом:

;

.

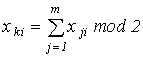
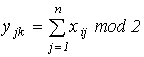
В этом случае не обнаруживаются только ошибки четной кратности с кратностью 4, 8, 16 и т.д., при которых происходит искажение символов с попарно одинаковыми индексами строк столбцов. Наименьшая избыточность кода получается в том случае, когда образуемая матрица является квадратной.

Недостатком такого кода является необходимость внесения задержки в передачу информации на время, необходимое для формирования матрицы.

Матричный код позволяет исправлять одиночные ошибки. Ошибочный элемент находится на пересечении строки и столбца, в которых имеется нарушение четности.

Коды с постоянным весом

Весом называется число единиц, содержащихся в кодовых комбинациях.

В коде «3 из 7» возможных комбинаций сто двадцать восемь (=128), а разрешенных кода только тридцать пять. Относительная избыточность _отн = 0,28.

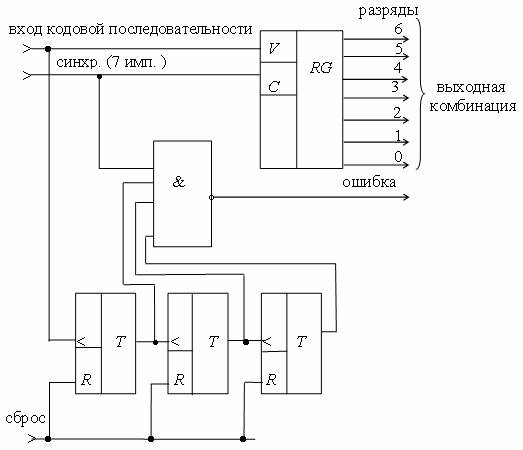
Схема устройства определения веса комбинаций кода «3 из 7» приведена на рис. 2.6.

Циклические коды

Циклические коды характеризуются тем, что при циклической перестановке всех символов кодовой комбинации данного кода образуется другая кодовая комбинация этого же кода.

— комбинация циклического кода;

— также комбинация циклического кода.

Например, комбинация 1001111 (п=7) будет представлена многочленом

При таком представлении действия над кодовыми комбинациями сводятся к действиям над многочленами. Эти действия производятся в соответствии с обычной алгебры, за исключением того, что приведение подобных членов осуществляется по модулю 2.

Обнаружение ошибок при помощи циклического кода обеспечивается тем, что в качестве разрешенных комбинаций выбираются такие, которые делятся без остатка на некоторый заранее выбранный полином G(x). Если принятая комбинация содержит искаженные символы, то деление на полином G(x) осуществляется с остатком. При этом формируется сигнал, свидетельствующий об ошибке. Полином G(x) называется образующим.

Построение комбинаций циклического кода возможно путем умножения исходной комбинации А(х) на образующий полином G(x) с приведением подобных членов по модулю 2:

Таким образом, все полиномы, отображающие комбинации циклического кода, будут иметь степень ниже п.

Часто в качестве полинома, на который осуществляется деление, берется полином G(x)=+1. При таком формировании кодовых комбинаций позиции информационных и контрольных символов заранее определить нельзя.

Большим преимуществом циклических кодов является простота построения кодирующих и декодирующих устройств, которые по своей структуре представляют регистры сдвига с обратными связями.

Число разрядов регистра выбирается равным степени образующего полинома.

Обратная связь осуществляется с выхода регистра на некоторые разряды через сумматоры, число которых выбирается на единицу меньше количества ненулевых членов образующего полинома. Сумматоры устанавливаются на входах тех разрядов регистра, которым соответствуют ненулевые члены образующего полинома.

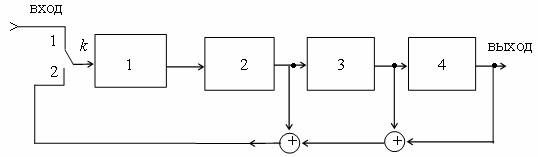
На рис. 2.7 приведена схема кодирующего регистра для преобразования четырехразрядной комбинации в семиразрядную.

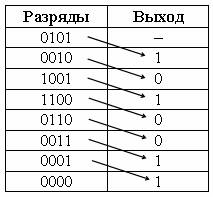
В табл. 2.3 показано, как путем сдвигов исходной комбинации 0101 получается комбинация циклического кода 1010011. п=7, k=4. Комбинация 0101, ключ в положении 1. В течение первых четырех тактов регистр будет заполнен, затем ключ переводится в положение 2. Обратная связь замыкается. Под действием семи сдвигающих тактов проходит формирование семиразрядного циклического кода.

Свойства циклического кода:

1) циклический код обнаруживает все одиночные ошибки, если образующий полином содержит более одного члена. Если G(x)=x+1, то код обнаруживает одиночные ошибки и все нечетные;

2) циклический код с G(x)=(x+1)G(x) обнаруживает все одиночные, двойные и тройные ошибки;

Источник