матрица м на н что строки что столбцы

Матрицы. Матрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов

Линейная алгебра

Матрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией.

Например, рассмотрим матрицу А размерности 2 х 3:

Матрицы А и В одного размера (m х n ) называют равными, если они поэлементно совпадают, т.е. a_ij = b_ij для 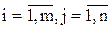, т.е. для любых i и j (можно записать «i, j).

Матрица-строка – это матрица, состоящая из одной строки, а матрица-столбец – это матрица, состоящая из одного столбца.

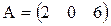
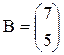
Например, — матрица-строка, а .

Квадратная матрица n-го порядка – это матрица, в число строк равно числу столбцов и равно n.

Например, 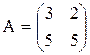— квадратная матрица второго порядка.

Диагональные элементы матрицы – это элементы, у которых номер строки равен номеру столбца (a_ij, i = j). Эти элементы образуют главную диагональ матрицы. В предыдущем примере главную диагональ образуют элементы a₁₁= 3 и a₂₂= 5.

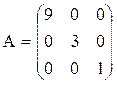
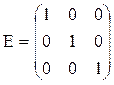
Диагональная матрица – это квадратная матрица, в которой все недиагональные элементы равны нулю. Например, — диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется единичной (обычно обозначаются буквой Е). Например, — единичная матрица третьего порядка.

Матрица называется нулевой, если все ее элементы равны нулю.

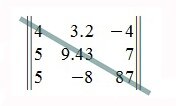
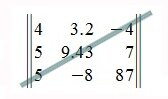
Квадратная матрица называется треугольной, если все ее элементы ниже (или выше) главной диагонали равны нулю. Например, 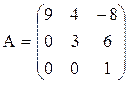— треугольная матрица третьего порядка.

Дата добавления: 2015-10-06 ; просмотров: 2723 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

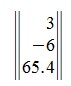
Матрица столбец

Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

Нулевая матрица

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

Главная диагональ матрицы

Побочная диагональ матрицы

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

Единичная матрица

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

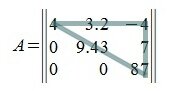
Верхняя треугольная матрица

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Источник

Матрицы: определение и основные понятия.

Определение матрицы

Количество строк и столбцов задают размеры матрицы.

Обозначение

A =		4	1	-7
		-1	0	2

Элементы матрицы

Элементы матрицы A_4×4:

A =		4	1	-7	2
		-1	0	2	44
		4	6	7	9
		11	3	1	5

Демонстрация нулевых и ненулевых строк матрицы:

Демонстрация нулевых и ненулевых столбцов матрицы:

4

1

-7

не не нулевой столбец

Диагонали матрицы

Демонстрация главной и побочной диагонали матрицы:

Источник

Основные сведения о матрицах

В этом разделе мы даем основные сведения о матрицах, необходимые для понимания статистики и анализа данных.

Матрицей размера m x n (читается m на n) называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

Числа, составляющие матрицу, называются элементами матрицы.

В сокращенной записи обозначаем A =( a_ij ); i =1,2,… m ; j =1,2,…, n

Приведем пример матрицы 2 на 2:

Наряду с круглыми скобками используются и другие обозначения матрицы:

Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, a_ij = b_ij для любых i =1,2,… m ; j =1,2,… n

Виды матриц

B=

Например,

Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.

Операции над матрицами

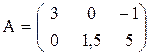
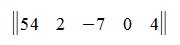
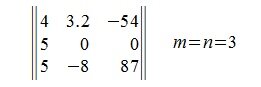
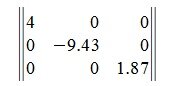
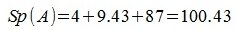
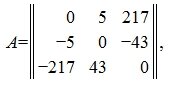
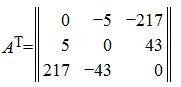
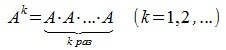
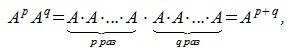
1. Умножение матрицы на число. Произведение матрицы А на число называется матрица B=A, элементы которой b_ij=a_ij для i=1,2,…m; j=1,2,…n

Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.

В частности, произведение матрицы А на число 0 есть нулевая матрица.

2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой c_ij=a_ij+b_ij для i=1,2,…m; j=1,2,…n (т.е. матрицы складываются поэлементно).

4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A_m ∙B _kназывается такая матрица C_m, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:

Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из этих операций):

Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:

a) Если АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать.

b) Если АВ и ВА существуют, то они могут быть матрицами разных размеров.

Из определения следует, что если матрица А имеет размер m , то транспонированная матрица А’ имеет размер n

В литературе встречаются и другие обозначения транспонированной матрицы, например, А Т

Источник

Знакомство с матрицами

Понятие и базовые операции.

Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:

Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.

Что такое матрица

Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.

Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.

Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.

В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.

В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.

Общая схема матрицы Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три

Простые операции с матрицами

Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.

И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.

Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений

Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

Пример умножения матрицы на число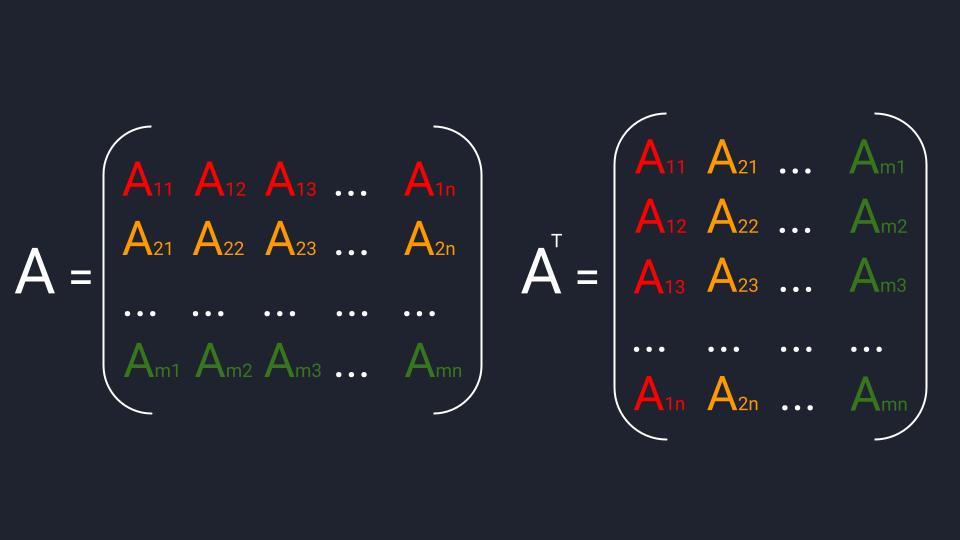

Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.

⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» 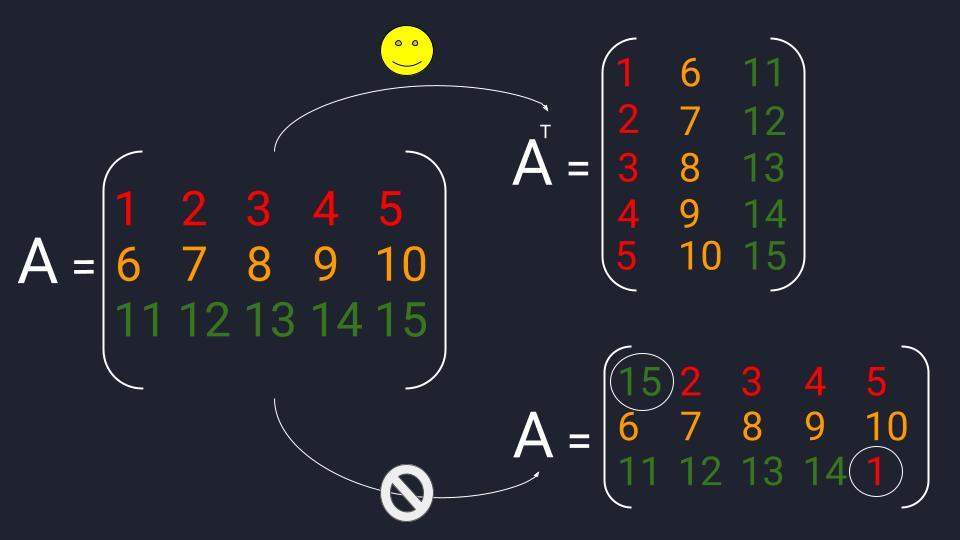Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил

Сложение и вычитание матриц

Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.

Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами Пример вычитания двух матриц

Умножение матриц

Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:

Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.

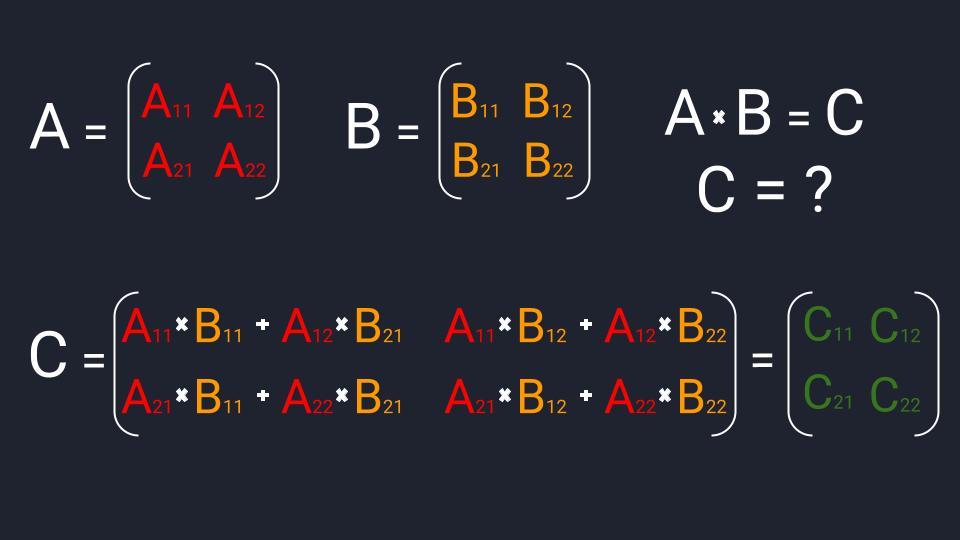Формула умножения матриц Пример умножения квадратных матриц размерностью 2×2

Что дальше

В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽

Источник

• ← С чем сделать морской коктейль
• get windowscapability такой запрос не поддерживается →

	0	1	-7
	0	0	2