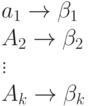найти среднюю длину кода сообщения
Алгоритм Хаффмана
Алгоритм Хаффмана (англ. Huffman’s algorithm) — алгоритм оптимального префиксного кодирования алфавита. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. Используется во многих программах сжатия данных, например, PKZIP 2, LZH и др.
Содержание
Определение [ править ]
Алгоритм построения бинарного кода Хаффмана [ править ]
Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:
Время работы [ править ]
Пример [ править ]
В дереве Хаффмана будет [math]5[/math] узлов:
| Узел | a | b | r | с | d |
|---|---|---|---|---|---|
| Вес | 5 | 2 | 2 | 1 | 1 |
| Узел | a | b | r | cd |
|---|---|---|---|---|
| Вес | 5 | 2 | 2 | 2 |
Затем опять объединим в один узел два минимальных по весу узла — [math]r[/math] и [math]cd[/math] :
| Узел | a | rcd | b |
|---|---|---|---|
| Вес | 5 | 4 | 2 |
Еще раз повторим эту же операцию, но для узлов [math]rcd[/math] и [math]b[/math] :
| Узел | brcd | a |
|---|---|---|
| Вес | 6 | 5 |
На последнем шаге объединим два узла — [math]brcd[/math] и [math]a[/math] :
| Узел | abrcd |
|---|---|
| Вес | 11 |
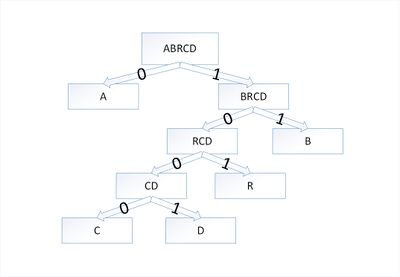
Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня):
| Символ | a | b | r | с | d |
|---|---|---|---|---|---|
| Код | 0 | 11 | 101 | 1000 | 1001 |
Корректность алгоритма Хаффмана [ править ]
Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.
[math]f[x]d_T(x) + f[y]d_T(y) = (f[x] + f[y])(d_
из чего следует, что
[math] B(T) = B(T’) + f[x] + f[y] [/math]
Рассчитать среднюю длину кода при методе Хаффмана
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Двухмерные массивы. Рассчитать среднюю температуру в первом столбце и среднюю во втором столбце
Здравствуйте. Мне нужна программа, в которой используются двухмерные массивы. Массив должен.
Определить среднюю длину слова в введенной текстовой строке, символы пунктуации на длину не влияют
определить среднюю длину слова в введенной текстовой строке, символы пунктуации на длину не влияют.
Рассчитать среднюю температуру за месяц
Написать функцию, находящую среднее значение в массиве с известным числом элементов. Написать.
Решение
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Рассчитать среднюю наработку на отказ
процессор имеет интенсивность отказа (λ) = 10^(-6) 1/c, интенсивность восстановления (µ) = 10^(-4).
Как рассчитать среднюю цену в 1с
Здравствуйте! Не могли бы подсказать, как сделать чтобы рассчитывало среднюю цену. Например если в.
StringGrid: Рассчитать среднюю температуру за месяц
как будет выглядеть код к этой задаче? Рассчитать среднюю температуру за месяц. Написать функцию.
Рассчитать среднюю ёмкость для трёх конденсаторов
Написать программу решения следующей задачи, используя модуль: Ёмкость плоского конденсатора.
Код Хаффмана
Построение кода Хаффмана для таблицы вероятностей.
Вот калькулятор, который рассчитывает коды Хаффмана для заданной вероятности символов.
Немного теории под калькулятором.
Код Хаффмана
Таблица вероятности символов
Таблица вероятности символов
Импортировать данные Ошибка импорта
Небольшой отрывок из Википедии.
Алгоритм Хаффмана — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.
Этот метод кодирования состоит из двух основных этапов:
Построение оптимального кодового дерева.
Построение отображения код-символ на основе построенного дерева.
Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (т. е. ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).
Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n0 потомков — символы из предыдущего шага и т. д.
Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от корня до листа дерева, соответствующего текущему символу, накапливая биты при перемещении по ветвям дерева (первая ветвь в пути соответствует младшему биту). Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.
Информационные технологии
Неравномерное кодирование. Средняя длина кодирования
В приведенных выше примерах кодирования все кодовые слова имели одинаковую длину. Однако это не является обязательным требованием. Более того, если вероятности появления сообщений заметно отличаются друг от друга, то сообщения с большой вероятностью появления лучше кодировать короткими словами, а более длинными словами кодировать редкие сообщений. В результате кодовый текст при определенных условиях станет в среднем короче.
Наиболее экономным является код с наименьшей средней длиной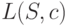 
. Сравним на примерах экономичность различных способов кодирования одного и того же источника.
Пусть источник содержит 4 сообщения 
с вероятностями 
. Эти сообщения можно закодировать кодовыми словами постоянной длины, состоящими из двух знаков, в алфавите 
в соответствии с кодовой таблицей.
 | 00 |
 | 01 |
| A_3 | 10 |
| A_4 | 11 |
Очевидно, что для представления (передачи) любой последовательности в среднем потребуется 2 знака на одно сообщение. Сравним эффективность такого кодирования с описанным выше кодированием словами переменной длины. Кодовая таблица для данного случая может иметь следующий вид.
| 0 |
| 1 |
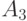 | 10 |
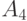 | 11 |
В этой таблице, в отличие от предыдущей, наиболее частые сообщения и кодируются одним двоичным знаком. Для последнего варианта кодирования имеем
в то время как для равномерного кода средняя длина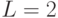 
(она совпадает с общей длиной кодовых слов). Из рассмотренного примера видно, что кодирование сообщений словами различной длины может дать суще-ственное (почти в два раза) увеличение экономичности кодирования.
Необходимо отметить, что неоднозначность декодирования слова появилась несмотря на то, что условие однозначности декодирования знаков (инъективность кодового отображения) выполняется.
Решение данной проблемы заключается в том, чтобы иметь возможность в любом кодовом тексте выделять отдельные кодовые слова без использования специальных разделительных знаков. Иначе говоря, необходимо, чтобы код удовлетворял следующему требованию: всякая последовательность кодовых знаков может быть единственным образом разбита на кодовые слова. Коды, для которых последнее требование выполнено, называются однозначно декодируемыми (иногда их называют кодами без запятой).
Рассмотрим код (схему алфавитного кодирования) 
, заданный кодовой таблицей
и различные слова, составленные из элементарных кодов.
Определение. Код 
называется однозначно декодируемым, если
Если таблица кодов содержит одинаковые кодовые слова, то есть если
то код заведомо не является однозначно декодируемым (схема не является разделимой). Такие коды далее не рассматриваются.
Префиксные коды
Наиболее простыми и часто используемыми кодами без специального разделителя кодовых слов являются так называемые префиксные коды [29].
Теорема 1. Префиксный код является однозначно декодируемым.
Множество кодовых слов можно графически изобразить как поддерево словарного дерева (рис.6.5). Для этого из всего словарного дерева следует показать только вершины, соответствующие кодовым словам, и пути, ведущие от этих вершин к корню дерева. Такое поддерево называют деревом кода или кодовым деревом.
Замечание. Свойство префиксности является достаточным, но не является необходимым для однозначной декодируемости.
Если код префиксный, то, читая кодовую запись подряд от начала, мы всегда сможем разобраться, где кончается одно кодовое слово и начинается следующее. Если, например, в кодовой записи встретилось кодовое обозначение 110, то разночтений быть не может, так как в силу префиксности наш код не содержит кодовых обозначений 1, 11 или, скажем, 1101. Именно так обстояло дело для рассмотренного выше кода, который очевидно является префиксным.
Алгоритм Хаффмана на пальцах
Вы вероятно слышали о Дэвиде Хаффмане и его популярном алгоритме сжатия. Если нет, то поищите информацию в интернете — в этой статье я не буду вас грузить историей или математикой. Сегодня я хочу просто попытаться показать вам практический пример применения алгоритма к символьной строке.
Примечание переводчика: под символом автор подразумевает некий повторяющийся элемент исходной строки — это может быть как печатный знак (character), так и любая битовая последовательность. Под кодом подразумевается не ASCII или UTF-8 код символа, а кодирующая последовательность битов.
К статье прикреплён исходный код, который наглядно демонстрирует, как работает алгоритм Хаффмана — он предназначен для людей, которые плохо понимают математику процесса. В будущем (я надеюсь) я напишу статью, в которой мы поговорим о применении алгоритма к любым файлам для их сжатия (то есть, сделаем простой архиватор типа WinRAR или WinZIP).
Идея, положенная в основу кодировании Хаффмана, основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код. Это нужно, так как мы хотим, чтобы, когда мы обработали весь ввод, самые частотные символы заняли меньше всего места (и меньше, чем они занимали в оригинале), а самые редкие — побольше (но так как они редкие, это не имеет значения). Для нашей программы я решил, что символ будет иметь длину 8 бит, то есть, будет соответствовать печатному знаку.
Мы могли бы с той же простотой взять символ длиной в 16 бит (то есть, состоящий из двух печатных знаков), равно как и 10 бит, 20 и так далее. Размер символа выбирается, исходя из строки ввода, которую мы ожидаем встретить. Например, если бы я собрался кодировать сырые видеофайлы, я бы приравнял размер символа к размеру пикселя. Помните, что при уменьшении или увеличении размера символа меняется и размер кода для каждого символа, потому что чем больше размер, тем больше символов можно закодировать этим размером кода. Комбинаций нулей и единичек, подходящих для восьми бит, меньше, чем для шестнадцати. Поэтому вы должны подобрать размер символа, исходя из того по какому принципу данные повторяются в вашей последовательности.
Для этого алгоритма вам потребуется минимальное понимание устройства бинарного дерева и очереди с приоритетами. В исходном коде я использовал код очереди с приоритетами из моей предыдущей статьи.
Предположим, у нас есть строка «beep boop beer!», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. После кодирования строка займёт 40 бит (на практике, в нашей программе мы выведем на консоль последовательность из 40 нулей и единиц, представляющих собой биты кодированного текста. Чтобы получить из них настоящую строку размером 40 бит, нужно применять битовую арифметику, поэтому мы сегодня не будем этого делать).
Чтобы лучше понять пример, мы для начала сделаем всё вручную. Строка «beep boop beer!» для этого очень хорошо подойдёт. Чтобы получить код для каждого символа на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей. Скоро вы увидите, для чего это нужно.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.
Для начала посчитаем частоты всех символов:
| Символ | Частота |
|---|---|
| ‘b’ | 3 |
| ‘e’ | 4 |
| ‘p’ | 2 |
| ‘ ‘ | 2 |
| ‘o’ | 2 |
| ‘r’ | 1 |
| ‘!’ | 1 |
После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета: 
Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь.
Повторим те же шаги и получим последовательно:
Ну и после того, как мы свяжем два последних элемента, получится итоговое дерево:
Теперь, чтобы получить код для каждого символа, надо просто пройтись по дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо:
Если мы так сделаем, то получим следующие коды для символов:
| Символ | Код |
|---|---|
| ‘b’ | 00 |
| ‘e’ | 11 |
| ‘p’ | 101 |
| ‘ ‘ | 011 |
| ‘o’ | 010 |
| ‘r’ | 1000 |
| ‘!’ | 1001 |
Чтобы расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву, сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для ‘b’, то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на ‘b’.
На практике, при реализации данного алгоритма сразу после построения дерева строится таблица Хаффмана. Данная таблица — это по сути связный список или массив, который содержит каждый символ и его код, потому что это делает кодирование более эффективным. Довольно затратно каждый раз искать символ и одновременно вычислять его код, так как мы не знаем, где он находится, и придётся обходить всё дерево целиком. Как правило, для кодирования используется таблица Хаффмана, а для декодирования — дерево Хаффмана.
Входная строка: «beep boop beer!»
Входная строка в бинарном виде: «0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000»
Закодированная строка: «0011 1110 1011 0001 0010 1010 1100 1111 1000 1001»
Как вы можете заметить, между ASCII-версией строки и закодированной версией существует большая разница.
Приложенный исходный код работает по тому же принципу, что и описан выше. В коде можно найти больше деталей и комментариев.
Все исходники были откомпилированы и проверены с использованием стандарта C99. Удачного программирования!
Чтобы прояснить ситуацию: данная статья только иллюстрирует работу алгоритма. Чтобы использовать это в реальной жизни, вам надо будет поместить созданное вами дерево Хаффмана в закодированную строку, а получатель должен будет знать, как его интерпретировать, чтобы раскодировать сообщение. Хорошим способом сделать это, является проход по дереву в любом порядке, который вам нравится (я предпочитаю обход в глубину) и конкатенировать 0 для каждого узла и 1 для листа с битами, представляющими оригинальный символ (в нашем случае, 8 бит, представляющие ASCII-код знака). Идеальным было бы добавить это представление в самое начало закодированной строки. Как только получатель построит дерево, он будет знать, как декодировать сообщение, чтобы прочесть оригинал.