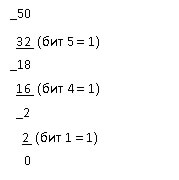найти вес кода заданного битовой строкой
Теория информации
3.9 Вес и расстояние Хэмминга. Способность кодов обнаруживать и исправлять ошибки
Число единиц в этой последовательности называется весом Хэмминга вектора u и обозначается как w(u).
Число разрядов, в которых эти слова различаются, называется расстоянием Хэмминга между u и v и обозначается как d(u, v).
Легко видеть, что расстояние между двоичными последовательностями u и v равно весу их поразрядной суммы, т. е.
Вероятность того, что слово v будет принято за u, равна
где p – вероятность правильной передачи бита сообщения; q=1—p – вероятность ошибки.
Задав линейный код, т. е., определив все 2 k кодовые слова, можно определить расстояние между всеми возможными парами кодовых слов, минимальное из них называется минимальным кодовым расстоянием dmin.
Нетрудно показать, что расстояние между нулевым кодовым словом и одним из кодовых слов, входящих в порождающую матрицу, равно dmin (по определению строки порождающей матрицы линейного блочного кода сами являются кодовыми словами данного кода).
Тогда, минимальное кодовое расстояние dmin равно минимальному весу Хэмминга для всех строк порождающей матрицы кода.
Для возможности обнаружения ошибки в одной позиции минимальное кодовое расстояние между словами должно быть больше 1, иначе ошибка в одной позиции может перевести одно кодовое слово в другое, что не даст её обнаружить.
Для обнаружения кодом ошибок кратности не больше l необходимо и достаточно, чтобы минимальное расстояние между его словами было l+1:
Для исправления кодом ошибок кратности, не больше l, необходимо и достаточно, чтобы наименьшее расстояние между его словами было 2l+1:
Установлено, что в линейном (k, n)-коде, минимальное расстояние между кодовыми словами которого равно 2l+1, значения n — длины кодовой последовательности, r=n—k — числа дополнительных разрядов и l — кратности ошибки, обнаруживаемой кодом, должны соответствовать неравенству

которое называется нижней границей Хэмминга.

Нижняя граница задаёт необходимые условия для помехоустойчивого кода с заданными характеристиками.
Верхняя граница задаёт достаточные условия для существования помехоустойчивого кода.
Для линейных блочных (k, n)-кодов с минимальным расстоянием dmin существует нижняя граница Плоткина, устанавливающая минимальное количество проверочных символов r при n ≥ 2dmin—1:

1) количество исходных кодовых комбинаций (число строк) порождающей матрицы равно k, т. е. количеству информационных элементов;
2) все кодовые комбинации порождающей матрицы должны быть различны, причём нулевая комбинация в их состав не включается;
3) все кодовые комбинации порождающей матрицы линейно независимы;
4) количество единиц в каждой кодовой комбинации порождающей матрицы должно быть ³ dmin;
5) кодовое расстояние между какими-либо парами кодовых слов должно быть ³ dmin.
Таким образом, порождающая матрица линейного систематического блочного кода составляется из двух подматриц: информационной подматрицы Ik×k (которую удобно представлять в виде единичной матрицы) и проверочной подматрицы Рk´r.
Найти вес кода заданного битовой строкой
Прежде, чем рассматривать выполнение машинных программ аппаратурой ЭВМ, рассмотрим представление в памяти машины чисел, а также алфавитно-цифровых символов. Это представление потребуется нам в дальнейшем при изучении машинных программ, а также обрабатываемых ими данных.
1.1 Двоичные числа
Чтобы сделать вычислительные системы более надежными и простыми, их аппаратура строится из простейших электронных схем, которые могут находиться только в двух состояниях. Одно из них обозначается 0, а другое – 1. Такая схема предназначена для длительного или краткого хранения самой мелкой единицы информации – бита (от «BInary digiT» – двоичная цифра).
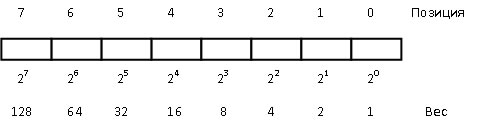
Любое число можно представить в виде цепочки битов. Такое представление числа называется двоичным числом. Цепочка из восьми битов называется байтом (рис. 1).

старший бит (бит 7) младший бит (бит 0)
Рис. 1. Пример байта
Величина двоичного числа определяется относительной позицией каждого бита и его значением. Позиционный вес младшего бита 2 о = 1(10), где 1(10) – единица в десятичной системе счисления. Следующий бит имеет вес 2 1 = 2(10). Вес любой позиции получается удвоением веса предыдущей позиции (рис. 2).
Рис. 2. Веса позиций байта
Для преобразования десятичного числа в двоичное можно использовать один из двух методов – метод деления и метод вычитания. Первый из этих методов широко используется в программах, выполняющих преобразование чисел из одной системы счисления в другую. Этот метод будет рассмотрен нами в других разделах, при описании соответствующих программ. Сейчас мы будем использовать метод вычитания, главное достоинство которого – наглядность. Согласно этому методу, для преобразования десятичного числа в двоичное надо сделать ряд вычитаний, каждое из которых даст значение одного бита.
Записывая 0 в остальные позиции битов (биты 0,2,3) получаем окончательный результат: 110010.
Для выполнения обратного преобразования следует сложить десятичные веса тех позиций, в которых стоит 1:
32 (бит 5) + 16 (бит 4) + 2 (бит 1) = 50
Байт может представлять десятичные положительные числа от 0 (00000000) до 255 (11111111). Число 255 может быть получено двумя способами: 1) суммированием весов всех битов байта; 2) по формуле 2 8 – 1, где 8 – номер первого бита, не вошедшего в состав байта.
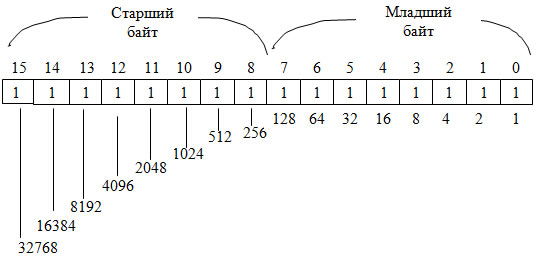
Машинным словом будем называть битовую строку длиной 16 битов. Одно слово содержит 2 байта (рис. 3). Каждый бит слова имеет свой вес. Просуммировав все веса, найдем максимальное целое число без знака, которое можно записать в одно слово, оно равно 2 16 – 1 = 65535.
Двоичное содержимое байта или слова может рассматриваться (интерпретироваться) как число без знака и как число со знаком. Число без знака занимает все 16 битов слова или 8 битов байта. Оно может быть только положительным. Просуммируем два таких числа:
Обратим внимание, что единица, появившаяся в старшем бите результата, свидетельствует лишь о возросшей величине результата, который для беззнаковых чисел может быть только неотрицательным.
Рис. 3. Веса позиций слова
все биты числа (в том числе и знаковый) инвертируются;
к полученному числу прибавляется 1.
Например, получим дополнительный код числа –65:
Для получения абсолютного значения отрицательного числа повторяют эти же самые два действия. Например:
Сумма +65 и –65 должна составить ноль:
В данном примере у нас произошли два интересных переноса: 1) в знаковый (7-й) разряд; 2) за пределы байта. Первая единица переноса обрабатывается как обычно, а вторая теряется. Оба переноса считаются правильными.
Отсюда видно, что нулевые биты в отрицательном двоичном числе фактически определяют его величину: рассмотрите весовые значения нулевых битов так, как если бы это были единичные биты, сложите эти значения и прибавьте 1.
Код Хэмминга (7; 4)
Структурно слова кода Хэмминга состоят из двух частей. Сначала идут информационные 4 бита, затем три бита проверочных. Будем обозначать информационные биты буквами ABCD, проверочные буквами xyz.
Таким образом слово кода Хэмминга имеет следующую структуру:
Для передачи 4 бит информации нам требуется передавать кодовое слово из целых 7 бит! Последние три бита в случае, когда ошибки отсутствуют, не несут никакой новой информации, ибо они зависят от первых 4. Однако если в кодовом слове из 7 бит произошла 1 ошибка, то исходные информационные 4 бита всё равно можно будет восстановить точно! В этом и состоит главная особенность самокорректирующихся кодов.
Для подсчёта проверочных бит можно использовать следующие формулы:
где n mod 2 означает остаток от деления числа n на 2.
К примеру, если информационный вектор есть ABCD = 1001, то кодовый вектор будет ABCDxyz = 1001 100
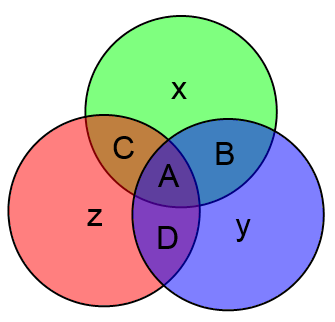
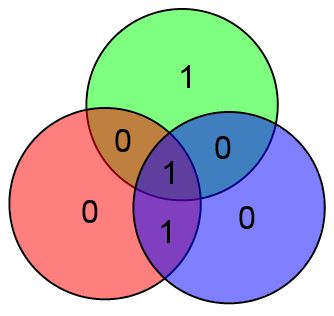
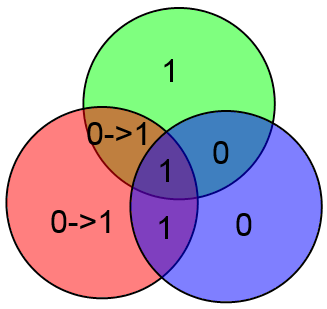
Вместо непонятных формул можно использовать следующую картинку:
Здесь всё очень просто. Подставляете вместо букв значения соответствующих битов и затем считаете значения x, y и z как сумму по модулю 2 тех информационных бит, которые есть в соответствующем круге.
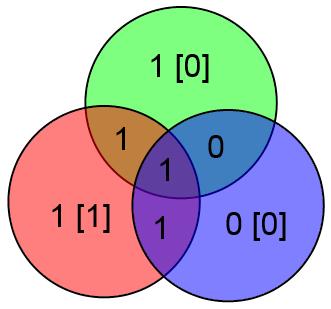
В приведённом выше примере будет:
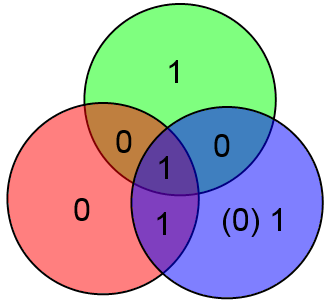
Куда более интересным является вопрос об исправлении ошибок. Очевидно, вывод об отсутствии ошибок приёмник может сделать просто взяв информационные биты ABCD, посчитав на их основе проверочные биты xyz и сравнить посчитанные проверочные биты с принятыми. Если есть ошибка, то часть проверочных битов не совпадёт.
Предположим что произошла ошибка в проверочном бите y и было принято слово 1001 110
В таком случае два проверочных бита сойдутся, а один нет. Этого вполне достаточно чтобы сделать вывод что нужно исправить бит y (для которого проверка не сошлась).
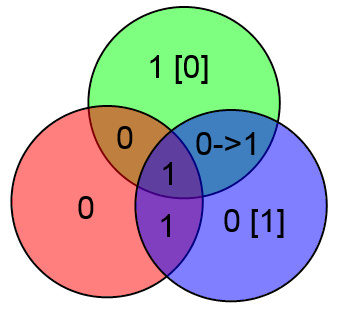
Наконец, отдельно рассмотрим бит A. Если в нём ошибка, то у нас не сойдутся все три проверки:
Увидев такое безобразие сразу же делаем вывод о том, что ошибка в бите A.
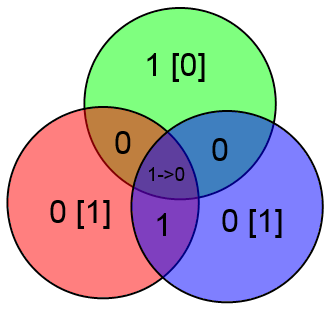
Таким образом, можно легко и просто вычислять локацию ошибки и исправлять её. Замечу что если ошибок больше одной, то описанный выше алгоритм сработает неверно. К примеру, допустим что произошли ошибки в битах C и z:
Проверочные биты y и z сойдутся, а бит x нет. Алгоритм исправит бит x и всё. Это вполне естественное поведение, т.к. если вероятность ошибки p 0).
Естественно, работать с цветными кругами удобно человеку, но неудобно компьютеру. У кодов Хэмминга есть одна особенность, которая позволяет их лёгкое декодирование на компьютере. Итак, рассмотрим следующий алгоритм:
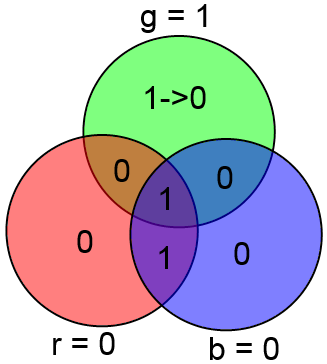
Определим числа g, b, r как сумму всех четырёх бит в кругах соответствующего цвета. Т.е.:
g = A + B + C + x mod 2,
b = A + B + D + y mod 2,
r = A + C + D + z mod 2.
Фактически каждый из этих бит можно определить как сумму соответствующего проверочного бита, вычисленного на основании принятых информационных бит, с принятым проверочным битом. Т.е. к примеру g есть сумма (A + B + C mod 2) (по этой формуле считался x на стороне передатчика) и принятого x. Аналогично b соответствует y, r соответствует z.
Если ошибок нет, то gbr = 000 (принятые проверочные биты сошлись с вычисленными на основе информационного вектора).
Если же есть 1 ошибка, то число gbr есть номер (в двоичной записи) ошибочного бита в векторе ABCxDyz.
В качестве примера рассмотрим уже знакомый нам вектор ABCDxyz = 1001 100, в котором произошла ошибка в бите x (четвёртый бит в векторе ABCxDyz). Посчитаем gbr:
gbr = 100 [2] = 4 [10]. Ошибка в 4 бите, которым и является x. Таким образом, для декодирования и исправления ошибки в кодовом слове длины 7 требуется лишь вычислить три суммы и из полученного числа несложной функцией получить местонахождение ошибки.
Код Хаффмана
Построение кода Хаффмана для таблицы вероятностей.
Вот калькулятор, который рассчитывает коды Хаффмана для заданной вероятности символов.
Немного теории под калькулятором.
Код Хаффмана
Таблица вероятности символов
Таблица вероятности символов
Импортировать данные Ошибка импорта
Небольшой отрывок из Википедии.
Алгоритм Хаффмана — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.
Этот метод кодирования состоит из двух основных этапов:
Построение оптимального кодового дерева.
Построение отображения код-символ на основе построенного дерева.
Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (т. е. ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).
Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n0 потомков — символы из предыдущего шага и т. д.
Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от корня до листа дерева, соответствующего текущему символу, накапливая биты при перемещении по ветвям дерева (первая ветвь в пути соответствует младшему биту). Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.
| Нить | Вес Хэмминга |
|---|---|
| 111 0 1 | 4 |
| 111 0 1 000 | 4 |
| 00000000 | 0 |
| 678 0 1234 0 567 | 10 |
| График подсчета населения (вес Хэмминга для двоичных чисел) для (десятичных) чисел от 0 до 256. |
СОДЕРЖАНИЕ
История и использование
Эффективное внедрение
| Выражение | Двоичный | Десятичная дробь | Комментарий | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | 01 | 10 | 11 | 00 | 10 | 11 | 10 | 10 | 27834 | Исходный номер |
| b0 = (a >> 0) & 01 01 01 01 01 01 01 01 | 01 | 00 | 01 | 00 | 00 | 01 | 00 | 00 | 1, 0, 1, 0, 0, 1, 0, 0 | Каждый другой бит от |
| b1 = (a >> 1) & 01 01 01 01 01 01 01 01 | 00 | 01 | 01 | 00 | 01 | 01 | 01 | 01 | 0, 1, 1, 0, 1, 1, 1, 1 | Остальные биты из |
| c = b0 + b1 | 01 | 01 | 10 | 00 | 01 | 10 | 01 | 01 | 1, 1, 2, 0, 1, 2, 1, 1 | Подсчет единиц в каждом 2-битном срезе |
| d0 = (c >> 0) & 0011 0011 0011 0011 | 0001 | 0000 | 0010 | 0001 | 1, 0, 2, 1 | Все остальные отсчитываются от c | ||||
| d2 = (c >> 2) & 0011 0011 0011 0011 | 0001 | 0010 | 0001 | 0001 | 1, 2, 1, 1 | Остальные отсчеты от c | ||||
| e = d0 + d2 | 0010 | 0010 | 0011 | 0010 | 2, 2, 3, 2 | Подсчет единиц в каждом 4-битном срезе | ||||
| f0 = (e >> 0) & 00001111 00001111 | 00000010 | 00000010 | 2, 2 | Все остальные считают от е | ||||||
| f4 = (e >> 4) & 00001111 00001111 | 00000010 | 00000011 | 2, 3 | Остальные отсчеты от e | ||||||
| g = f0 + f4 | 00000100 | 00000101 | 4, 5 | Подсчет единиц в каждом 8-битном срезе | ||||||
| h0 = (g >> 0) & 0000000011111111 | 0000000000000101 | 5 | Все остальные считают от g | |||||||
| h8 = (g >> 8) & 0000000011111111 | 0000000000000100 | 4 | Остальные отсчеты от g | |||||||
| i = h0 + h8 | 0000000000001001 | 9 | Подсчет единиц во всем 16-битном слове | |||||||
Если разрешено большее использование памяти, мы можем вычислить вес Хэмминга быстрее, чем описанные выше методы. Имея неограниченную память, мы могли бы просто создать большую таблицу поиска веса Хэмминга для каждого 64-битного целого числа. Если мы можем сохранить таблицу поиска функции Хэмминга для каждого 16-битного целого числа, мы можем сделать следующее, чтобы вычислить вес Хэмминга для каждого 32-битного целого числа.
Muła et al. показали, что векторизованная версия popcount64b может работать быстрее, чем специальные инструкции (например, popcnt на процессорах x64).
Минимальный вес
Языковая поддержка
Некоторые компиляторы C предоставляют встроенные функции, обеспечивающие подсчет битов. Например, GCC (начиная с версии 3.4 в апреле 2004 г.) включает встроенную функцию, __builtin_popcount которая будет использовать инструкцию процессора, если она доступна, или эффективную реализацию библиотеки в противном случае. LLVM-GCC включает эту функцию с версии 1.5 в июне 2005 года.
В Java структура данных растущего битового массива BitSet имеет BitSet.cardinality() метод, который подсчитывает количество установленных битов. Кроме того, существует Integer.bitCount(int) и Long.bitCount(long) функция для подсчета бит в примитивных 32-битных и 64-битных числах, соответственно. Кроме того, BigInteger целочисленный класс произвольной точности также имеет BigInteger.bitCount() метод подсчета битов.
В Python у этого int типа есть bit_count() метод для подсчета количества установленных битов. Эта функция является новой в Python 3.10, выпуск которой запланирован на 2021 год.
Начиная с GHC 7.4, в базовом пакете Haskell есть popCount функция, доступная для всех типов, которые являются экземплярами Bits класса (доступны из Data.Bits модуля).
MySQL версии SQL языка обеспечивает в BIT_COUNT() качестве стандартной функции.
Fortran 2008 имеет стандартную внутреннюю элементарную функцию, popcnt возвращающую количество ненулевых битов в целочисленном (или целочисленном массиве).
FreePascal реализует popcnt начиная с версии 3.0.