обратный код в троичной системе
Учебник | Троичная система счисления
Троичная система счисления — позиционная система счисления с целочисленным основанием, равным 3.
Существует в двух вариантах: несимметричная и симметричная.
В несимметричной троичной системе счисления чаще применяются цифры <0,1,2>, а в троичной симметричной системе счисления знаки <-,0,+>, <-1,0,+1>, <1,0,1>, <1,0,1>,
Изменение знака числа в симметричном коде равносильно потритной инверсии, т.е. взаимозамене всех “+” на “-” и всех “-” на “+”.
В отличие от двоичной, это арифметика чисел со знаком, причем знаком числа оказывается цифра старшего из его значащих (ненулевых) разрядов. Проблемы чисел со знаком, не имеющей в двоичном коде совершенного решения, в троичном симметричном коде просто нет, чем и обусловлены его принципиальные преимущества.
В цифровой технике система счисления с основанием b реализуется регистрами, состоящими из наборов триггеров, каждый из которых может принимать b различных состояний, кодирующих цифры числа. При этом особое значение приобретает экономичность системы счисления — возможность представления как можно большего диапазона чисел с использованием как можно меньшего общего количества состояний.
Если общее количество состояний равно m, то количество триггеров равно m/b, а количество представимых ими чисел соответственно — b^(m/b). Как функция от b, это выражение достигает максимума при b равном числу e = 2,718281828…. При целых значениях b максимум достигается для b = 3. Таким образом, наиболее экономичной является троичная система счисления (используемая в троичных ЭВМ), следом за которой идут двоичная система счисления (традиционно используемая в большинстве распространённых ЭВМ) и четверичная система счисления.
Немного философии
Бинарная логика, являющаяся основой современной вычислительной техники, воспринимается сегодня как некая аксиома, истинность которой не подвергается сомнению. И действительно, кодирование информации с помощью наличия или отсутствия сигнала кажется самым подходящим способом реализации цифровых систем. Но так ли это?
Почему именно двоичная логика стала базой современных ЭВМ? Ответ представляется очевидным. Исторически математическая логика опиралась на идею «третьего не дано», сводя процесс логических умозаключений к бинарным решениям.
Простота бивалентности действительно неплохо описывает логические реалии жизни. Стоит вспомнить семафоры, пешеходные переходы и тумблеры «вкл-выкл». Бинарность неплохо управляет повседневностью.
В русской историко-математической литературе «задача о гирях» известна под названием «задачи Баше-Менделеева», названной так в честь французского математика 17 в. Баше де Мезириака, который разместил эту задачу в своем «Сборнике приятных и занимательных задач» (1612 г.) и блестящего русского химика Дмитрия Ивановича Менделеева, который интересовался этой задачей будучи директором Главной Палаты мер и весов России.
Хронология
Томас Фоулер работал банковским служащим и по роду деятельности был вынужден производить сложные вычисления. Чтобы облегчить и ускорить свою работу, он сделал таблицы для счета степенями двойки и тройки, а позже опубликовал эти таблицы в виде брошюры.
Преимущества троичных ЭВМ
Троичные ЭВМ (компьютеры) обладают рядом преимуществ по сравнению с двоичными ЭВМ (компьютерами).
При сложении тритов в троичных полусумматорах и в троичных сумматорах количество сложений приблизительно в 1,5 раза меньше, чем при сложении битов в двоичных полусумматорах и в двоичных сумматорах, и, следовательно, быстродействие при сложении приблизительно в 1,5 раза больше.
При применении симметричной троичной системы счисления и сложение и вычитание производится в одних и тех же двухаргументных (двухоперандных) полусумматорах-полувычитателях или полных трёхаргументных (трёхоперандных) сумматорах-вычитателях без преобразования отрицательных чисел в дополнительные коды, то есть ещё немного быстрее, чем в двоичных полусумматорах и в двоичных полных сумматорах с преобразованием отрицательных чисел в дополнительные коды.
Троичная логика целиком включает в себя двоичную логику, как центральное подмножество, поэтому троичные ЭВМ (компьютеры) могут делать почти всё, что делают двоичные ЭВМ (компьютеры), плюс возможности троичной логики.
Обратный и дополнительный коды двоичных чисел



Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


TREX: 27-ричная симметричная система счисления
Каждый специалист по компьютерам знает, насколько сложно работать с длинными последовательностями нулей и единиц. На помощь ему приходят восьмеричная и шестнадцатиричная системы счисления, обеспечивающие более компактное представление информации.
С троичной системой счисления ситуация хуже: есть несколько способов представления троичных чисел и есть несколько способов компактной записи троичных чисел, но они имеют недостатки, усложняющие работу с ними.
Система кодирования TREX разработана для компактного отображения симметричной троичной системы счисления при ее использовании в компьютерных системах
Замечания
В данной статье речь идет только о симметричной троичной системе счисления, использующей значения <-1, 0, +1>.
Недостатки предлагаемых на сегодняшний момент 9-ти и 27-ричных систем кодирования троичных чисел будут упомянуты ниже в сравнении с системой TREX.
Проблематика
При разработке ПО для работы с троичными компьютерами встает вопрос вывода информации на различные устройства отображения информации. При этом информация должна выводиться упорядоченно, чтобы при печати, например, дампов одинаковые разряды чисел располагались на одинаковых позиция строки.
Работа с троичной логикой очень непривычна даже для опытных программистов, поэтому для повышения удобства работы, минимизации человеческих ошибок и сокращения времени освоения троичного компьютера (который когда-нибудь уже будет создан) требуется система кодирования, обладающая простотой, наглядностью и односимвольностью ( отображением одного разряда одним символом, желательно из стандартного набора ASCII)
Представление троичных чисел
Для записи симметричной троичной системы счисления удобной формы отображения на экране компьютера можно добиться, используя алфавит <-, 0, +>.
Компактное представление троичных чисел
Поскольку с длинными последовательностями знаков «-», «0» и «+» работать неудобно (как и с длинными последовательностями «0» и «1» в двоичной системе счисления), то должна быть возможность компактного отображения информации (по аналогии с HEX-кодом).
По аналогии с названием HEX, для представляемой системы счисления предлагается использовать название TREX.
Описание системы кодирования
Система TREX использует следующий алфавит:
Троичные единицы данных и их запись в TREX
Трит
Единичный троичный разряд, который в симметричной троичной системе счисления может принимать значения <-1, 0, +1>. Для удобного отображения на устройствах вывода информации целесообразно использовать символы <-, 0, +>соответственно.
Трибл
Трибл (3 троичных разряда или 1/3 часть трайта) кодируется одним символом TREX
Трайт
Преимущества перед имеющимися 9-ти и 27-ричными системами кодирования
Предлагаемая система кодирования выгодно отличается от предлагавшихся до этого 9-ти и 27-ричных систем следующими особенностями:
односимвольностью — каждое значение отображается одним символом, не требуется вводить двухсимвольные обозначения.
Существующие системы кодирования:
существует 9-ричная система, использующая алфавит <-4,-3,-2,-1,0,1,2,3,4>
естественностью – для записи не применяются специальные символы.
Существующие системы кодирования:
существует вариант 9-тиричной системы счисления, использующий специальные символы с верхней чертой (не знаю, как нарисовать символы с верхним подчеркиванием, поэтому вставил картинку):
Свойства односимвольности и естественности очень удобны при компактном отображении на экране троичных дампов без использования специальных шрифтов.
визуальной симметричностью — для противоположных значений используются одни и те же символы с разным регистром, в отличие от систем, где противоположные значения обозначаются разными символами.
Существующие системы кодирования:
существуют 9-ричная система, использующая алфавит
Свойство визуальной симметричности позволяет выполнять очевидные операции с троичными числами «в уме»
Пример:
-(AdFGhb) = aDfgHB
вычисление модуля числа – модуль числа равен самому числу, если старшая цифра положительная или инвертированному числу, если она отрицательная
Пример:
mod (Mf0) = Mf0
mod (a0H) = A0h
Пример:
Mfa 00a
+ => + => 00G
mFH 00H
Пример:
Mfa > Mma
afa > bfa
Выводы
Предлагаемая система кодирования позволит:
упорядочить отображение троичной информации на экране компьютера (выровненные дампы)
уменьшить число выводимых знаков по сравнению с поразрядным выводом троичных данных
облегчить работу с троичными числами широкому кругу специалистов
уменьшить количество ошибок при разработке программного обеспечения для троичных компьютеров или их эмуляторов.
Троичная уравновешенная система счисления и применение её в ЭВМ
Вы будете перенаправлены на Автор24
Классическая двоичная система счисления, как мы знаем, используется для представления информации в компьютере, однако она имеет существенные недостатки, которые влияют на скорость работы процессора.
Один из недостатков – это проблематичное представление отрицательных чисел.
В целях повышения быстродействия компьютера, работа которого основывается на использовании двоичной системы, разработчики ввели особое беззнаковое представление отрицательных целых чисел — так называемый дополнительный код. В результате операция вычитания стала выполняться аналогично операции сложения.
$01111111=0\cdot (-128)+1\cdot 64+1\cdot 32+. +1\cdot 1=127$, а
$11111111=1\cdot (-128)+1\cdot 64+. +1\cdot 1=-1$.
Готовые работы на аналогичную тему
Симметричную систему счисления называют также уравновешенной, она была предложена математиком Леонардо Пизано Фибоначчи ($1170 – 1228$) для решения «задачи о гирях».
Приведем несколько других записей результатов взвешивания:
Симметричная троичная система наиболее экономна с точки зрения представления чисел.
Если не использовать значение «неизвестно», троичная логика сводится к обычной двоичной логике.
Представления чисел в троичной системе
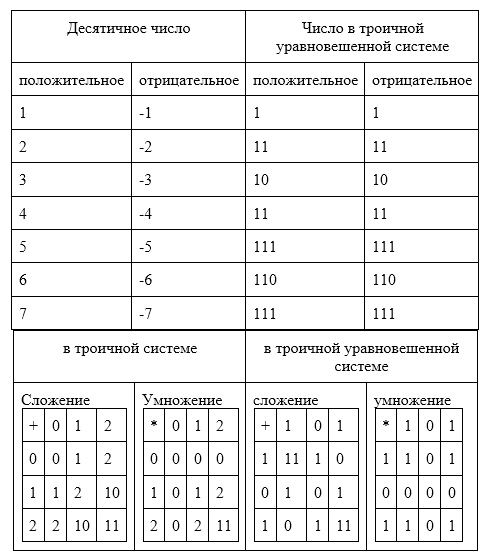
В таблице приведены примеры представления целых положительных чисел в несимметричной троичной системе счисления:
В следующей таблице приведены примеры представления чисел в троичной уравновешенной системе счисления. Глядя на таблицу, понятно, почему эту систему назвали уравновешенной, или симметричной. Очевидно, знак для представления отрицательных чисел не нужен!
Представление отрицательных чисел
Преимущества троичной уравновешенной системы счисления
Для изменения знака у представляемого числа на противоположный необходимо изменить знаки у всех цифр, из которых оно состоит. Это свойство увеличивает число операций при перемене знака (в несимметричных системах изменяется только один знаковый разряд), но в то же время повышает надёжность при сбоях в одном или более разрядах.
Процесс округления числа в данной системе счисления заключается в следующем: абсолютная величина части числа, представленной отбрасываемыми младшими цифрами, никогда не превосходит половины абсолютной величины части числа, соответствующей младшей значащей цифре младшего из сохраняемых разрядов. Следовательно, в результате отбрасывания младших цифр числа получаем наиболее выгодное при данном количестве оставшихся цифр приближение, соответственно округление не требуется.