перцептрон на питоне код

Русские Блоги

Модель персептрона Розенблатта на основе Python

Персептрон Розенблатта

Реализация Python

Реализация нейрона Розенблатта

С помощью математической модели персептрона Розенблатта его можно очень просто использовать. numpy В библиотеке реализована функция перцептрона.

Набор данных за два месяца

В этом тесте используется набор данных раз в два месяца, как показано на следующем рисунке:

Конструктор определяет информацию за один месяц:

Gen_SemicircleData() Генератор, используемый для генерации определенного количества точек в форме одного месяца, процесс должен использоваться в первую очередь random.uniform() Сгенерируйте случайный радиус внутри радиуса, а затем сгенерируйте случайное смещение x в пределах положительного и отрицательного радиуса, вычислите смещение y по теореме Пифагора, то есть сгенерируйте случайную точку, попадающую в форму одного месяца, и Сгенерируйте абсолютные координаты этой точки в соответствии с ориентацией yield возвращение

Среда обучения и тестирования Rosenblatt

Создавайте обучающие и тестовые среды, вызывая коды Rosenblatt и набора данных, и используйте matplotlib Визуализировать рисунок

Сначала создайте нейроны и наборы данных

Затем используйте набор данных для обучения и сохраните данные обучения.

Проведите прямую линию результата по данным, полученным в процессе обучения

использовать matplotlib Рисование, plt.plot() Используется для рисования линейной диаграммы, цветовая конфигурация может относиться кВот， plt.scatter() Используется для рисования точечных диаграмм, plt.show() Показать нарисованное изображение, подробнее matplotlib Рисунок можно ссылаться наВотс участиемВот

результат

Полученное изображение выглядит следующим образом:

Красная линия представляет результат обучения перцептрона. Видно, что граница между двумя с половиной месяцами хорошо разделена.

Интеллектуальная рекомендация

Взаимодействие между WebView и JS

Предисловие Теперь многие приложения имеют встроенные веб-страницы (гибридное приложение), например, многие платформы электронной коммерции, Taobao, JD, Juhuasuan и т. Д., Как показано ниже. Вышеупомя.

LeetCode 31. Next Permutation

Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers. If such arrangement is not possible, it must rearrange it as the lowest possib.

Zoho Survey: как заставить людей более охотно отвечать на ваши вопросы

Джанго исследование параллелизма

Возможность параллелизма django действительно вызывает беспокойство, здесь используйте nginx + uwsgi для обеспечения высокого параллелизма Одновременная способность Nginx чрезвычайно высока, а единств.

Установка и настройка среды системы Wy PyQt

С настроенной средой Python вы можете выполнить следующие шаги для установки PyQt5 1. Установите PyQt5 Откройте cmd и введите команду: 2.Установить Qt Designer Введите ту же команду: Это завершает мон.

Источник

Как создать нейронную сеть многослойный перцептрон на Python

Данная статья шаг за шагом проведет вас по программе на Python, которая позволит нам обучить нейронную сеть и выполнить сложную классификацию.

Это 12-я статья в серии о разработке нейронных сетей. С остальными статьями вы можете ознакомиться выше, в меню с содержанием.

В данной статье мы применим знания, полученные нами при изучении нейронных сетей перцептрон, и узнаем, как реализовать нейросеть на знакомом языке: Python.

Разработка понятного кода на Python для нейронных сетей

Недавно я просмотрел немало онлайн-ресурсов по нейронным сетям, и, хотя, несомненно, в них есть много полезной информации, я не был удовлетворен найденными мною программными реализациями. Они всегда были или слишком сложными, или недостаточно интуитивно понятными. Когда я писал свою нейронную сеть на Python, я на самом деле хотел сделать что-то, что могло бы помочь людям узнать о том, как работает система, и как теория нейронных сетей переводится на язык программных инструкций.

Однако иногда между ясностью и эффективностью кода существует обратная зависимость. Программа, которую мы обсудим в этой статье, однозначно не оптимизирована для быстрой работы. Оптимизация является серьезной проблемой в области нейронных сетей; реальные приложения могут потребовать огромного количества обучения, и, следовательно, тщательная оптимизация может привести к значительному сокращению времени обработки. Тем не менее, для простых экспериментов, подобных тем, которые мы будем проводить, обучение не займет много времени, и нет оснований делать упор на методиках программирования, которые способствуют скорости, а не простоте и понятности.

Полный код программы на Python приведен в конце статьи. Код выполняет как обучение, так и проверку. Данная статья посвящена обучению, а валидацию мы обсудим позже. В любом случае, во фрагменте программы, выполняющем проверку, не так много функционала, который не покрыт во фрагменте, выполняющем обучение.

Размышляя над кодом, вы, возможно, захотите оглянуться на немного сумбурную, но очень информативную диаграмму архитектуры плюс терминологии, которую я представил в части 10.

Рисунок 1 – Демонстрация терминов на диаграмме конфигурации нейросети

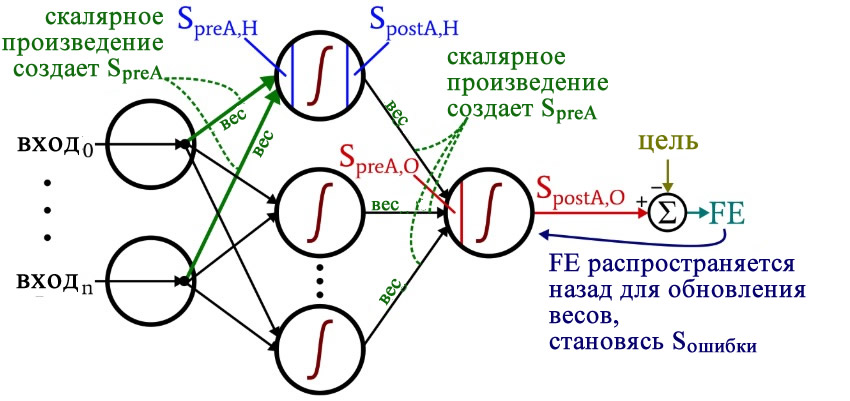
Подготовка функций и переменных

Библиотека NumPy широко используется для расчетов в нейросети, а библиотека Pandas дает мне удобный способ импортировать данные обучения из файла Excel.

Как вы уже знаете, для активации мы используем функцию логистической сигмоиды. Для расчета значений постактивации нам нужна сама логистическая функция, а для обратного распространения необходима производная логистической функции.

Затем мы выбираем скорость обучения, размерность входного слоя, размерность скрытого слоя и количество эпох. Для реальных нейронных сетей важно обучение в течение нескольких эпох, потому что это позволяет вам извлечь больше информации из ваших обучающих данных. Когда вы генерируете обучающие данные в Excel, вам не нужно запускать несколько эпох, потому что вы можете легко создать больше обучающих выборок.

Функция np.random.uniform() заполняет наши две матрицы весов случайными значениями от –1 до +1 (обратите внимание, что матрица весов между скрытым и выходным слоями на самом деле представляет собой просто массив, поскольку у нас только один выходной узел). Оператор np.random.seed(1) приводит к тому, что случайные значения становятся одинаковыми при каждом запуске программы. Начальные значения весов могут оказать существенное влияние на конечную производительность обученной сети, поэтому, если вы пытаетесь оценить, как другие переменные улучшают или ухудшают производительность, вы можете раскомментировать эту инструкцию и тем самым устранить влияние случайной инициализации весовых коэффициентов.

И в конце я создаю пустые массивы для значений преактивации и постактивации в скрытом слое.

Импорт обучающих данных

Обработка прямого распространения

Вычисления, которые создают выходное значение, и в которых данные перемещаются слева направо на типовой схеме нейронной сети, составляют фрагмент «прямого распространения» работы системы. Вот код «прямого распространения»:

После этого мы готовы вычислить сигнал преактивации для выходного узла (снова используя скалярное произведение), и мы применяем функцию активации для генерирования сигнала постактивации. Затем, чтобы вычислить итоговую ошибку, мы вычитаем целевое значение из значения полученного сигнала постактивации выходного узла.

Обратное распространение

После того, как мы выполнили расчеты для прямого распространения, настало время изменить направление. Во фрагменте программы с обратным распространением мы перемещаемся к весам от скрытых узлов к выходному узлу, а затем к весам от входного слоя к скрытому слою, перенося при этом информацию об ошибке для эффективного обучения сети.

У нас есть два слоя для циклов for : один для весовых коэффициентов между скрытым и выходным слоями и один для весовых коэффициентов между входным и скрытым слоями. Сначала мы генерируем сигнал ошибки (S_ошибки, S_error ), который нам нужен для вычисления обоих градиентов, gradient_HtoO (от скрытого слоя к выходному) и gradient_ItoH (от входного слоя к скрытому), а затем мы обновляем весовые коэффициенты, вычитая градиент, умноженный на скорость обучения.

Обратите внимание, как веса между входным и скрытым слоями обновляются внутри цикла для значений между скрытым и выходным слоями. Мы начинаем с сигнала ошибки, который ведет обратно к одному из скрытых узлов, затем распространяем этот сигнал ошибки на все входные узлы, которые подключены к одному конкретному скрытому узлу:

Рисунок 2 – Обратное распространение ошибки

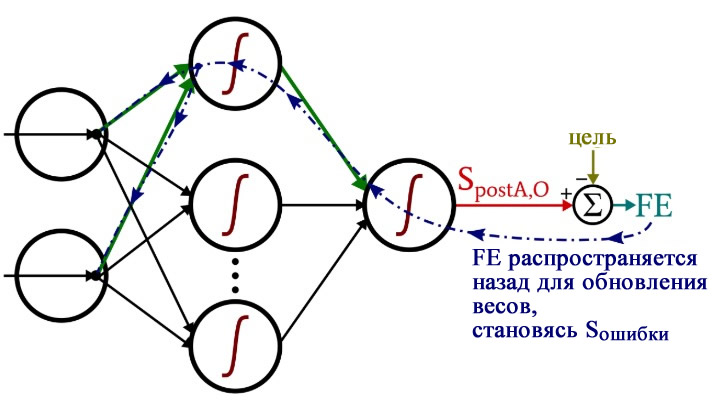
После того, как все весовые коэффициенты (как ItoH (от входного слоя к скрытому), так и HtoO (от скрытого слоя к выходному)), связанные с этим одним скрытым узлом, были обновлены, мы возвращаемся к началу и начинаем снова для следующего скрытого узла.

Также обратите внимание, что веса ItoH модифицируются перед весами HtoO. Мы используем текущий вес HtoO при расчете градиента, поэтому до выполнения расчетов мы не хотим изменять веса HtoO.

Заключение

Интересно задуматься о том, сколько теории ушло в эту относительно короткую программу на Python. Я надеюсь, что этот код на самом деле поможет вам понять, как мы можем программно реализовать нейронную сеть многослойный перцептрон.

Источник

Однослойный персептрон на языке Python без сторонних модулей

Я написал уникальный, не имеющий аналогов в мире однослойный персептрон без использования сторонних модулей. Для чего? Что бы всем показывать свою статью на Хабрахабре, очевидно же. Это не перевод и не копия чьей-нибудь статьи, всё своё.

Итак, весь код:

Функция train — обучает, predict — обрабатывает входные данные уже обученными синапсами и выдает ответ, trainmass — запускает обучение по всем входным данным(2 — это количество выходных данных, 4 — количество данных в примере, 1 — это лерн рейт, 60000 — количество циклов обучения), create — создает массив случайных синапсов для обучения.

В этом примере массив X имеет 4 набора данных и массив y 4 набора выходных данных.

После запуска имеем вывод:

Первый массив — это ответ на входные данные X[0] — [0.1, 0.2, 0.3, 0.4].
Второй массив — это ответ на данные которые не были в обучающей выборке [0.5, 0.6, 0.7, 0.8].

Как видите персептрон продолжил числовой ряд почти верно с небольшими отклонениями.
Немного разберем принцип его работы. Персептрон получает что-то похожее на систему линейных уравнений:

И методом обратного распространения ошибки находит соответствующие x1, x2, x3, x4.
Для второго выходного значения создаются другие y1, y2, y3, y4.

Я не стану описывать функцию активации — сигмоид. Если вы разберетесь в этом простом коде вам станет понятно.

Однослойный персептрон может решать только линейные задачи. Для нелинейности нужно добавить еще слой или несколько слоев. Если будет много комментариев, я напишу двухслойную модель.

Источник

Как обучить простую нейронную сеть перцептрон

В данной статье представлен код на Python, который позволяет автоматически генерировать веса для простой нейронной сети.

Добро пожаловать в серию статей по нейронным сетям перцептрон. Если вы хотите начать с самого начала или перейти вперед, ознакомьтесь с остальными статьями в меню с содержанием серии выше, в начале статьи.

Классификация с помощью однослойного перцептрона

В предыдущей статье была представлена простая задача классификации, которую мы рассмотрели с точки зрения обработки сигналов на базе нейросети. Математическая связь, необходимая для этой задачи, была настолько простой, что я смог спроектировать сеть, просто подумав о том, как определенный набор весов позволил бы выходному узлу правильно классифицировать входные данные.

Это сеть, которую я разработал:

Рисунок 1 – Пример разработанной нейросети

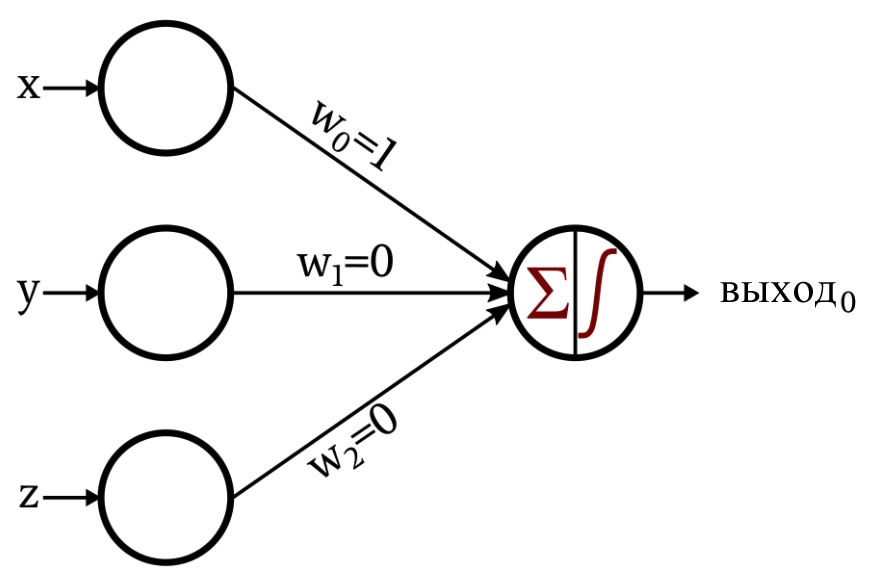
Функция активации в выходном узле – это единичная ступенчатая функция:

Обсуждение стало немного интереснее, когда я представил сеть, которая создала свои собственные веса с помощью процедуры, известной как обучение:

Рисунок 4 – Результаты обучения нейросети перцептрон

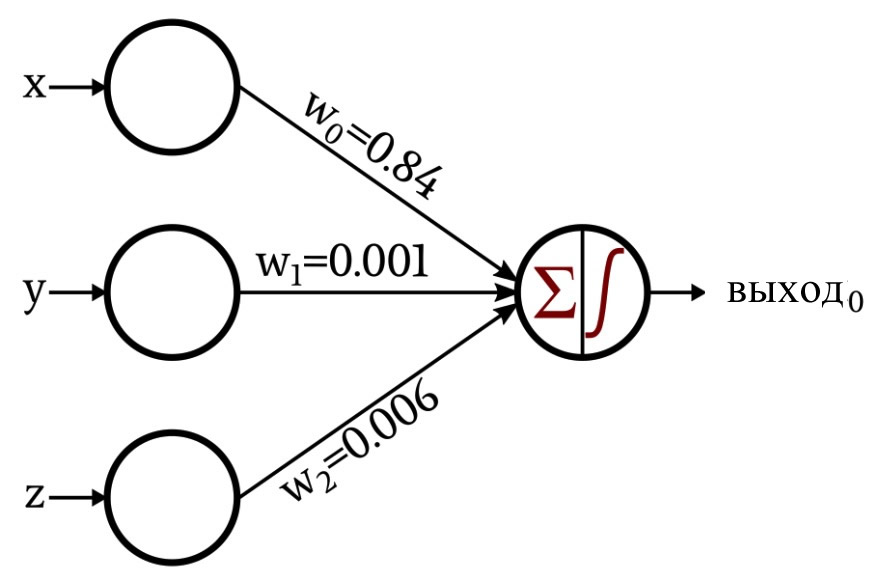
В оставшейся части данной статьи мы рассмотрим код на Python, который я использовал для получения этих весов.

Нейронная сеть на Python

Давайте внимательнее посмотрим на эти инструкции.

Настройка сети и организация данных

Размерность регулируется. Наши входные данные, если вы помните, состоят из трехмерных координат, поэтому нам необходимо три входных узла. Эта программа не поддерживает несколько выходных узлов, но мы включим регулируемую выходную размерность в будущем эксперименте.

Мы обсудим скорость обучения в следующей статье.

Я использую библиотеку pandas для импорта обучающих данных из электронной таблицы Excel. Следующая статья более подробно расскажет о тренировочных данных.

Набор обучающих данных включает в себя входные значения и соответствующие выходные значения. Первая инструкция выделяет выходные значения и сохраняет их в отдельном массиве, а следующая инструкция удаляет выходные значения из исходного набора обучающих данных.

Я преобразую набор обучающих данных, который в настоящее время является структурой данных pandas, в массив numpy, а затем просматриваю длину одного из столбцов, чтобы определить, сколько точек данных доступно для обучения.

Расчет выходных значений

Продолжительность одной тренировки определяется количеством доступных обучающих данных. Тем не менее, вы можете продолжить оптимизацию весов, обучая нейросеть несколько раз, используя один и тот же набор данных – преимущества обучения не исчезают просто потому, что нейросеть уже видела эти обучающие данные. Каждый полный проход через весь обучающий набор называется эпохой.

Процедура, содержащаяся в этом цикле, выполняется один раз для каждой строки в обучающем наборе, где «строка» относится к группе значений входных данных и соответствующему выходному значению (в нашем случае входная группа состоит из трех чисел, представляющих компоненты x, y и z точки в трехмерном пространстве).

Оператор if-else применяет единичную ступенчатую функцию активации: если сумма меньше нуля, значение, сгенерированное выходным узлом, равно 0; если сумма равна или больше нуля, выходное значение равно единице.

Обновление весов

Когда первый расчет выходных значений завершен, у нас есть весовые значения, но они не помогли нам достичь правильной классификации, потому что они были сгенерированы случайным образом. Мы превращаем нейронную сеть в эффективную систему классификации, многократно изменяя веса таким образом, чтобы они постепенно отражали математическое соотношение между входными данными и искомыми выходными значениями. Изменение веса достигается путем применения следующего правила обучения для каждой строки в обучающем наборе:

\[w_ <новый>= w+(\alpha\times\delta\times вход)\]

Вот как я реализовал это правило обучения на Python:

Заключение

Теперь у вас есть код, который вы можете использовать для обучения однослойного перцептрона с одним выходным узлом. Более подробно о теории и практике обучения нейронных сетей мы расскажем в следующей статье.

Источник

Как реализовать алгоритм перцептрона с нуля в Python

Дата публикации 2016-11-02

Это модель одного нейрона, которая может использоваться для задач классификации двух классов и обеспечивает основу для дальнейшей разработки гораздо более крупных сетей.

В этом руководстве вы узнаете, как реализовать алгоритм Perceptron с нуля с помощью Python.

После завершения этого урока вы узнаете:

Описание

В этом разделе дается краткое введение в алгоритм Perceptron и набор данных Sonar, к которым мы позже применим его.

Алгоритм персептрона

Перцептрон вдохновлен обработкой информации одной нервной клетки, называемой нейроном.

Нейрон принимает входные сигналы через свои дендриты, которые передают электрический сигнал в тело клетки.

Аналогичным образом, Perceptron получает входные сигналы от примеров тренировочных данных, которые мы взвешиваем и объединяем в линейное уравнение, называемое активацией.

Затем активация преобразуется в выходное значение или прогноз с использованием передаточной функции, такой как пошаговая передаточная функция.

Таким образом, Перцептрон является алгоритмом классификации для задач с двумя классами (0 и 1), где линейное уравнение (например, или гиперплоскость) может использоваться для разделения двух классов.

Это тесно связано с линейной регрессией и логистической регрессией, которые делают предсказания аналогичным образом (например, взвешенная сумма входных данных).

Вес алгоритма Perceptron должен быть оценен на основе ваших тренировочных данных с использованием стохастического градиентного спуска.

Стохастический градиентный спуск

Это включает в себя знание формы стоимости, а также производной, чтобы из заданной точки вы знали градиент и могли двигаться в этом направлении, например, вниз к минимальному значению.

В машинном обучении мы можем использовать технику, которая оценивает и обновляет веса на каждой итерации, называемую стохастическим градиентным спуском, чтобы минимизировать ошибку модели в наших обучающих данных.

Этот алгоритм оптимизации работает так, что каждый обучающий экземпляр показывается модели по одному. Модель делает прогноз для обучающего экземпляра, вычисляется ошибка, и модель обновляется, чтобы уменьшить ошибку для следующего прогнозирования.

Эта процедура может использоваться, чтобы найти набор весов в модели, который приводит к наименьшей ошибке для модели в данных обучения.

Для алгоритма Perceptron каждая итерация весов (вес) обновляются с использованием уравнения:

Сонар Набор данных

Прогнозируя класс с наибольшим количеством наблюдений в наборе данных (M или мин), алгоритм нулевого правила может достичь точности 53%.

Вы можете узнать больше об этом наборе данных наUCI хранилище машинного обучения, Вы можете скачать набор данных бесплатно и поместить его в свой рабочий каталог с именем файлаsonar.all-data.csv,

Руководство

Этот урок разбит на 3 части:

Эти шаги дадут вам основу для реализации и применения алгоритма Perceptron к вашим собственным задачам прогнозного моделирования классификации.

1. Делать прогнозы

Первым шагом является разработка функции, которая может делать прогнозы.

Это будет необходимо как при оценке значений весов кандидатов при стохастическом градиентном спуске, так и после того, как модель будет завершена, и мы хотим начать делать прогнозы на тестовых данных или новых данных.

Ниже приведена функция с именемпредсказать, ()это предсказывает выходное значение для строки, заданной набором весов.

Первый вес всегда является смещением, поскольку он является автономным и не отвечает за конкретное входное значение.

Мы можем создать небольшой набор данных для проверки нашей функции прогнозирования.

Мы также можем использовать предварительно подготовленные веса, чтобы делать прогнозы для этого набора данных.

Собрав все это вместе, мы можем проверить нашипредсказать, ()функция ниже.

Есть два входных значения (X1а такжеX2) и три значения веса (смещение,w1а такжеw2). Уравнение активации, которое мы смоделировали для этой задачи:

Или с конкретными значениями веса, которые мы выбрали вручную, как:

Запустив эту функцию, мы получим прогнозы, которые соответствуют ожидаемому результату (Y) ценности.

Теперь мы готовы реализовать стохастический градиентный спуск, чтобы оптимизировать наши значения веса.

2. Веса тренировочной сети

Мы можем оценить значения веса для наших тренировочных данных, используя стохастический градиентный спуск.

Стохастический градиентный спуск требует двух параметров:

Они вместе с данными обучения будут аргументами функции.

В функции нам нужно выполнить 3 цикла:

Как видите, мы обновляем каждый вес для каждой строки в тренировочных данных, каждую эпоху.

Веса обновляются в зависимости от ошибки, допущенной моделью. Ошибка рассчитывается как разница между ожидаемым выходным значением и прогнозом, сделанным с использованием весов-кандидатов.

Существует один вес для каждого входного атрибута, и они обновляются согласованным образом, например:

Смещение обновляется аналогичным образом, за исключением того, что без ввода, поскольку оно не связано с конкретным значением ввода:

Теперь мы можем собрать все это вместе. Ниже приведена функция с именемtrain_weights ()который вычисляет значения веса для учебного набора данных с использованием стохастического градиентного спуска.

Вы можете видеть, что мы также отслеживаем сумму квадратов ошибок (положительное значение) для каждой эпохи, чтобы мы могли распечатать хорошее сообщение в каждом внешнем цикле.

Мы можем протестировать эту функцию на том же небольшом измышленном наборе данных сверху.

Мы используем скорость обучения 0,1 и обучаем модель только для 5 эпох, или 5 воздействий весов на весь набор обучающих данных.

При выполнении примера в каждую эпоху печатается сообщение с ошибкой суммы квадратов для этой эпохи и окончательным набором весов.

Вы можете увидеть, как алгоритм очень быстро изучает проблему.

Теперь давайте применим этот алгоритм к реальному набору данных.

3. Моделирование набора данных сонара

В этом разделе мы обучим модель персептрона с использованием стохастического градиентного спуска на наборе данных сонара.

В этом примере предполагается, что CSV-копия набора данных находится в текущем рабочем каталоге с именем файла.sonar.all-data.csv,

Сначала загружается набор данных, строковые значения преобразуются в числовые, а выходной столбец преобразуется из строк в целочисленные значения от 0 до 1. Это достигается с помощью вспомогательных функций.load_csv (),str_column_to_float ()а такжеstr_column_to_int ()загрузить и подготовить набор данных.

Мы будем использовать перекрестную проверку в k-кратном размере для оценки эффективности изученной модели на невидимых данных. Это означает, что мы будем строить и оценивать k моделей и оценивать производительность как среднюю ошибку модели. Точность классификации будет использоваться для оценки каждой модели. Эти поведения представлены вcross_validation_split (),accuracy_metric ()а такжеevaluate_algorithm ()вспомогательные функции.

Мы будем использоватьпрогнозировать () иtrain_weights ()функции, созданные выше, чтобы обучить модель и новыйперсептрон ()функция, чтобы связать их вместе.

Ниже приведен полный пример.

Значение k, равное 3, использовалось для перекрестной проверки, давая каждому сгибу 208/3 = 69,3 или чуть менее 70 записей для оценки на каждой итерации. Скорость обучения 0,1 и 500 тренировочных эпох была выбрана с небольшими экспериментами.

Вы можете попробовать свои собственные конфигурации и посмотреть, сможете ли вы побить мой счет.

Выполнение этого примера печатает оценки для каждого из 3-х сгибов перекрестной проверки, а затем печатает среднюю точность классификации.

Мы можем видеть, что точность составляет около 72%, что выше базового значения чуть более 50%, если мы только предсказывали мажоритарный класс, используя алгоритм нулевого правила.

расширения

В этом разделе перечислены расширения к этому учебнику, которые вы, возможно, захотите изучить.

Вы исследовали какое-либо из этих расширений?
Дайте мне знать об этом в комментариях ниже.

Обзор

В этом руководстве вы узнали, как реализовать алгоритм Perceptron с использованием стохастического градиентного спуска с нуля с помощью Python.

У вас есть вопросы?
Задайте свой вопрос в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Источник