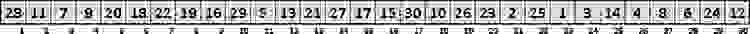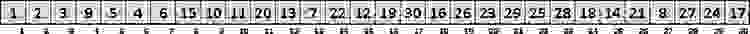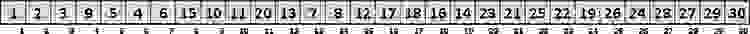пирамидальная сортировка java код
J-сортировка

Пирамидальная сортировка (она же сортировка кучей) – классический алгоритм который, пожалуй, должен знать любой программист. Старая добрая «пирамидка» примечательна тем, что в независимости от набора данных у неё одна и та же сложность по времени (причём, очень пристойная) – O(n log n). Лучших и вырожденных случаев для неё нет.
С момента изобретения метода (а в этом году алгоритм празднует свой полувековой юбилей) было немало охочих кардинально оптимизировать процесс накладывания сортирующих куч. Тернарная пирамидальная сортировка, плавная сортировка, сортировка декартовым деревом – вот неполный список инноваций. Перечисленные алгоритмы хотя при тестировании и опережают оригинал по абсолютной скорости кто на 12, а кто и на 25%, в оценке временной сложности всё равно крутятся вокруг O(n log n). При этом данные методы весьма изощрённо реализованы.
Своё видение пирамидальной сортировки предложил и скромный труженик Университета Манитобы Джейсон Моррисон. При этом способ в некоторых случаях по скорости приближается к O(n).
HeapSort
Для тех кто не в теме, кратенько обрисую как работает пирамидальная сортировка.

Массив можно отсортировать, если на его основе строить и перестраивать сортирующее дерево, известное как двоичная куча или просто пирамида.
Что есть сортирующее дерево? Это дерево, у которого любой родитель больше (или меньше, смотря в какую сторону оно сортирующее) чем его потомки.
Как из обычного дерева сделать сортирующее дерево? Очень просто – нужно двигаться от потомков вверх к родителям и если потомок больше родителя, то менять местами. Если такой обмен произошёл, опустившегося на один уровень родителя нужно сравнить с потомками ниже – может и там тоже будет повод для обмена.
Преобразовывая неотсортированную часть массива в сортирующее дерево, в итоге в корень «всплывёт» наибольший элемент. Обмениваем максимум с последним ключом неотсортированного подмассива. Структура перестанет быть сортирующим деревом, но в качестве моральной компенсации его неотсортированная часть станет меньше на один узел. К этой неотсортированной части заново применим всю процедуру, то есть преобразуем её в сортирующее дерево с последующей перестановкой найденного максимума в конец. И так действуем до тех пор, пока неотсортированная часть не скукожится до одного-единственного элемента.
Подход, что и говорить, остроумный, но при этом специалисты по алгоритмам отмечают у сортировки кучей целую кучу недостатков, как-то: неустойчивость, хаотичность выборки, нечувствительность к почти упорядоченным массивам и пр. Смущает всех также неулучшаемая скорость O(n log n), демонстрируемая сортировкой абсолютно при любых наборах входящих данных.

Выдающиеся умы computer science предлагают различные мозговыносящие идеи (тернарные пирамиды, числа Леонардо, декартовы деревья) с помощью которых можно улучшить алгоритм. Джейсон Моррисон (Jason Morrison, сортировка названа в честь автора) предложил нечто противоположное – для оптимизации надо не усложнять, а максимально упрощать.
JSort
Канадский учёный пришёл к выводу, что заново перестраивать кучу для каждого элемента – дорогое удовольствие. Так уж ли необходимо массив из n элементов радикально перелопачивать n раз?
Если для массива построить всего пару куч (нисходящую и восходящую), то это значительно его упорядочит в обоих направлениях.

Сначала нужно осуществить построение невозрастающей кучи. В результате меньшие элементы повсплывают в верхние узлы пирамиды (что будет соответствовать левой половине массива), наименьший элемент вообще окажется в корне. Чем выше элементы находятся в сортирующем дереве – тем более упорядоченной будет соответствующая часть массива. Элементы находящиеся ближе к листьям дерева (им будет соответствовать вторая половина массива) будут иметь менее упорядоченный вид, поскольку они не сравнивались друг с другом, а просто были оттеснены на задворки в результате перемещения их родителей.
Для наведения относительного порядка в правой части массива следует построить кучу ещё раз, во всём противоположную первой. Во-первых, эта куча должна быть неубывающей (мы ведь теперь хотим разобраться с крупными по значению ключами). Во-вторых, она должна быть «зеркальной» к массиву, то есть её корень должен соответствовать не первому, а последнему элементу и выстраивать дерево следует, перебирая массив от конца к началу.
Соорудив такие себе близняшки-пирамидки, получаем во многом упорядоченный массив. Довершает дело сортировка вставками. Этот алгоритм имеет весьма скромную среднюю сложность по времени O(n 2 ), но творит чудеса на массивах, которые уже почти отсортированы. Их сортировка вставками щёлкает как орешки.
Сложность по времени
Попробуем оценить при самом благоприятном раскладе. Однократное пирамидостроение – это O(n). Куч мы наложили две, так что получаем O(2n). Почти упорядоченный массив сортировка вставками может отсортировать за рекордные O(n). Общая сложность получается O(3n), что тоже самое что и O(n).
Впрочем, на практике всё выглядит скромнее. Возьмём, например, такой неотсортированный массив, содержащий числа от 1 до 30:
Построим обычную невозрастающую кучу:
Первая треть массива приняла вполне благообразный вид, в середине – кто в лес кто по дрова, конец массива пока тоже не впечатляет.
Построим теперь «зеркальную» неубывающую кучу:
Обратите внимание на ключ со значением 20.Почему этот элемент застрял в первой трети массива? Банально не повезло – перед построением «зеркальной» неубывающей кучи все родители вверх по ветке оказались больше по значению (в корне сейчас 17, но этот ключ утонет в левой половине дерева и уступит место 30). Поэтому в пирамиде ему не суждено возвыситься хотя бы на ступеньку.
Чем длиннее массив, тем чаще такие вырожденные узлы будет возникать. А значит, в средней полосе длинных массивов сортировке вставками придётся изрядно потрудиться. Подаваемый ей массив для обработки будет не то чтобы почти отсортированным, а скорее почти почти отсортированным. На очень длинных списках временная сложность у Insertion Sort будет, конечно, не её средние/худшие O(n 2 ), но и до O(n) будет далеко.
Между прочим
Есть ещё один алгоритм сортировки с очень похожим наименованием – J sort, которую разработал Джон Коен (John Cohen). Это тоже гибридный алгоритм, используется для обработки двусвязных списков. Сочетает в себе нитевидную сортировку (Strand sort) и сортировку перетасовкой (Shuffle sort). Но это уже другая история.
Сортировка n-нарной пирамидой
Сортировку кучей (она же — пирамидальная сортировка) на Хабре уже поминали добрым словом не раз и не два, но это всегда была достаточно общеизвестная информация. Обычную бинарную кучу знают все, но ведь в теории алгоритмов также есть:
n-нарная куча; куча куч, основанная на числах Леонардо; дерамида (гибрид кучи и двоичного дерева поиска); турнирная мини-куча; зеркальная (обратная) куча; слабая куча; юнгова куча; биномиальная куча; и бог весть ещё какие кучи…
И умнейшие представители computer science в разные годы предложили свои алгоритмы сортировки с помощью этих пирамидальных структур. Кому интересно, что у них получилось — для тех начинаем небольшую серию статей, посвящённую вопросам сортировки с помощью этих структур. Мир куч многообразен — надеюсь, вам будет интересно.

Статья написана при поддержке компании EDISON.
Мы очень любим теорию алгоритмов! 😉
Есть такой класс алгоритмов — сортировки выбором. Общая идея — неупорядоченная часть массива уменьшается за счёт того, что в ней ищутся максимальные элементы, которые из неё переставляются в увеличивающуюся отсортированную область.
Сортировка обычным выбором — это брутфорс. Если в поисках максимумов просто линейно проходить по массиву, то временнáя сложность такого алгоритма не может превысить O(n 2 ).
Наиболее эффективный способ работать с максимумами в массиве — это организовать данные в специальную древовидную структуру, известную как куча. Это дерево, в котором все родительские узлы не меньше чем узлы-потомки.
Другие названия кучи — пирамида, сортирующее дерево.
Давайте разберём, как это можно легко и почти бесплатно представить массив в виде дерева.
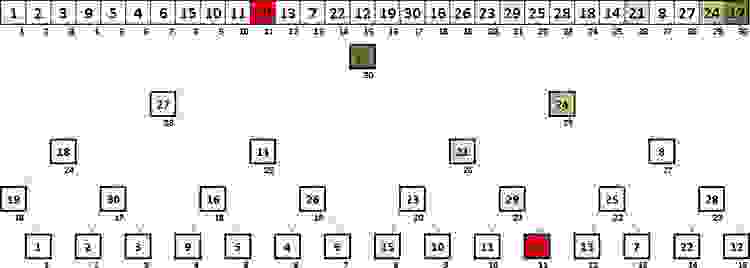
Возьмём самый первый элемент массива и будем считатть, что это корень дерева — узел 1-го уровня. Следующие 2 элемента — это узлы 2-го уровня, правый и левый потомки корневого элемента. Следующие 4 элемента — это узлы 3-го уровня, правые/левые потомки второго/третьего элемента массива. Следующие 8 элементов — узлы 4-го уровня, потомки элементов 3-го уровня. И т.д. На этом изображении узлы бинарного дерева наглядно расположены строго под соответствующими элементами в массиве:
Хотя, деревья на диаграммах чаще изображают в такой развёртке:
Если смотреть под таким углом, то тогда понятно почему сортировку кучей называют пирамидальной сортировкой. Хотя, это примерно тоже самое, как если шахматного слона называть офицером, ладью — турой, а ферзя — королевой.
Индексы потомков для i-го элемента определяются элементарно (если индекс самого первого элемента массива считать равным 0, как принято в подавляющем большинстве языков программирования):
Левый потомок: 2 × i + 1
Правый потомок: 2 × i + 2
Если получающиеся по этим формулам индексы потомков выходят за пределы массива, значит у i-го элемента потомков нет. Также может статься что у i-го элемента есть левый потомок (приходится на самый последний элемент массива, в котором нечётное количество элементов), но уже нет правого.
Итак, любой массив можно легко представить в виде дерева, однако это пока ещё не куча, потому что, в массиве некоторые элементы-потомки могут оказаться больше чем их элементы-родители.
Чтобы наше дерево, созданное на основе массива, стало кучей, его нужно как следует просеять.
Просейка
Душой сортировки кучей является просейка.
Просеивание для элемента состоит в том, что если он меньше по размеру чем потомки, объединённых в неразрывную цепочку, то этот элемент нужно переместить как можно ниже, а бо́льших потомков по ветке поднять наверх на 1 уровень.
На изображении показан путь просейки для элемента. Синим цветом обозначен элемент для которого осуществляется просейка. Зелёный цвет — бо́льшие потомки вниз по ветке. Они будут подняты на один уровень вверх, поскольку по величине превосходят синий узел, для которого делается просейка. Сам элемент из самого верхнего синего узла будет перемещён на место самого нижнего потомка из зелёной цепочки.
Просейка нужна для того, чтобы из обычного дерева сделать сортирующее дерево и в дальнейшем поддерживать дерево в таком (сортирующем) состоянии.
На этом изображении элементы массива перераспределены так, что он уже разложен именно в кучу. Хотя массив раскладывается в сортирующее дерево, сам он пока что не отсортирован (ни по возрастанию ни по убыванию), хотя все потомки в дереве меньше чем их родительские узлы. Но зато самый максимальный элемент в сортирующем дереве всегда находится в главном корне, что очень важно.
Сортировка кучей :: Heapsort
Алгоритм на самом деле простой:
Код на Питоне классической реализации пирамидальной сортировки:
Сложность алгоритма
Чем хороша простая куча — её не нужно отдельно хранить, в отличие от других видов деревьев (например, двоичное дерево поиска на основе массива прежде чем использовать нужно сначала создать). Любой массив уже является деревом, в котором прямо на ходу можно сразу определять родителей и потомков. Сложность по дополнительной памяти O(1), всё происходит сразу на месте.
Итоговая сложность по времени: O(n log n) + O(n log n) = O(n log n).
При этом у пирамидальной сортировки нет ни вырожденных ни лучших случаев. Любой массив будет обработан на приличной скорости, но при этом не будет ни деградации ни рекордов.
Сортировка кучей в среднем работает несколько медленнее чем быстрая сортировка. Но для quicksort можно подобрать массив-убийцу, на котором компьютер зависнет, а вот для heapsort — нет.
| Сложность по времени | |||
|---|---|---|---|
| Худшая | Средняя | Лучшая | |
| Сортировка кучей | O(n log n) | ||
| Быстрая сортировка | O(n 2 ) | O(n log n) | O(n) |
Сортировка тернарной кучей :: Ternary heapsort
Давайте рассмотрим троичную кучу. От двоичной она, вы не поверите, отличается только тем, что у родительских узлов максимум не два, а три потомка. В тернарной куче для i-го элемента индексы его трёх потомков вычисляются аналогично (если у первого элемента индекс = 0):
Левый потомок: 3 × i + 1
Средний потомок: 3 × i + 2
Правый потомок: 3 × i + 3
(Если индексы начинать с 1, как на анимациях в этой статье, то в этих формулах надо просто отнять единицу).
С одной стороны заметно уменьшается количество уровней в дереве по сравнению с двоичной кучей, что означает, что в среднем при просейке будет происходить меньше свопов. С другой стороны, для нахождения минимального потомка понадобится больше сравнений — ведь потомков теперь не по два, а по три. В общем, в плане сложности по времени — где-то находим, где-то теряем, однако в целом тоже самое. Данные в тернарной куче сортируется немного быстрее чем в бинарной, но это убыстрение весьма незначительное. Во всех вариациях пирамидальной сортировки разработчики алгоритмов предпочитают брать именно двоичный вариант, потому что троичный якобы сложнее в реализации (хотя это «сложнее» заключается в добавлении в алгоритм буквально пары-тройки дополнительных строк), а выигрыш по скорости минимален.
Сортировка n-нарной кучей :: N-narny heapsort
Разумеется, можно не останавливаться на достигнутом и адаптировать сортировку кучей для любого числа потомков. Может быть, если и дальше увеличивать количества потомков, можно существенно повысить скорость процесса?
Для i-го элемента массива индексы (если отсчитывать их с нуля) его N потомков вычисляются очень просто:
1-й потомок: N × i + 1
2-й потомок: N × i + 2
3-й потомок: N × i + 3
…
N-й потомок: N × i + N
Код на Python сортировки N-нарной кучей:
Впрочем, больше — не значит, лучше. Если довести ситуацию до предела и брать N потомков для массива из N элементов, то сортировка кучей деградирует до сортировки обычным выбором. Причём это будет ещё и ухудшенная версия сортировки выбором, так как будут совершаться бессмысленные телодвижения: просейка сначала будет ставить максимум на первое место в массиве, а потом будет отправлять максимум в конец (в selection sort отправка максимума в конец происходит сразу).
Если троичная куча минимально обгоняет двоичную, то четверичная уже проигрывает. Поиск максимального потомка среди нескольких становится слишком дорогим.
Трейлер следующей серии
Кликните по анимации для перехода в статью со следующей сортировкой кучей
Ссылки